Il moto rettilineo
Il moto rettilineo di un punto materiale si svolge su una retta, sulla quale ho fissato una origine e un verso in modo arbitrario.
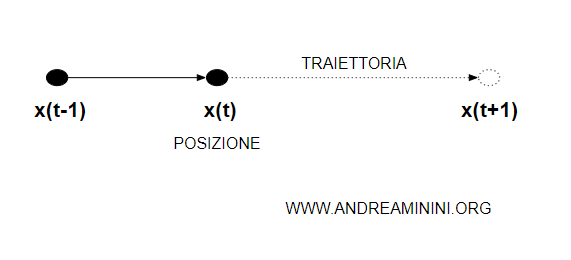
Il moto del punto è descrivibile con una singola funzione del tempo x(t).
Dove x(t) è la posizione del punto sulla retta nell'istante t.
Tipi di moti rettilinei
Il moto rettilineo è detto
- moto rettilineo uniforme se la velocità è costante
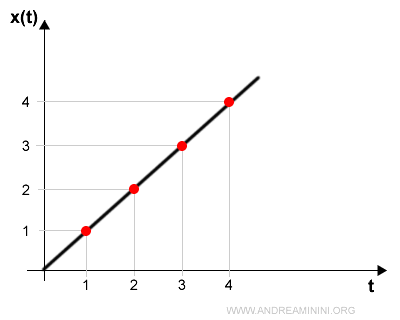
- moto rettilineo uniformemente accelerato se la velocità cambia ma l'accelerazione è costante
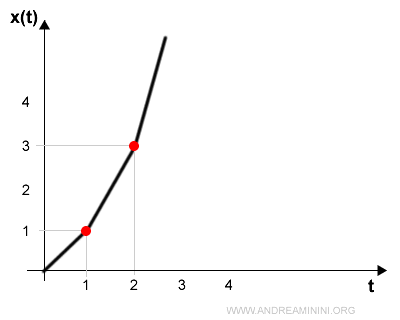
- moto rettilineo smorzato esponenzialmente se la velocità si riduce in modo esponenziale
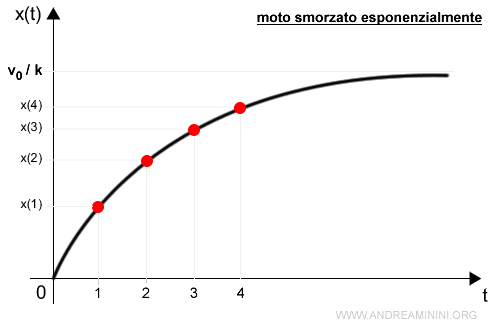
- moto rettilineo vario se l'accelerazione cambia nel corso del tempo senza seguire una relazione particolare.
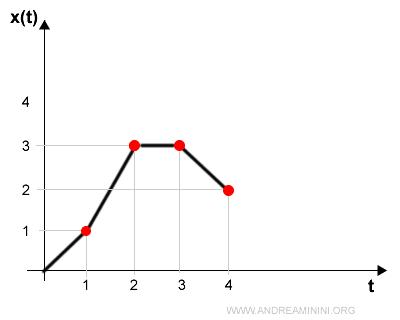
Come rappresentare il moto rettilineo
In un moto rettilineo lo spazio si riduce a una sola dimensione.
Quindi il moto è descritto da una sola coordinata x(t) che indica la posizione del punto in funzione del tempo.

Sulla retta fisso un'origine e un verso.
Poi fisso un'unità di misura delle grandezze fisiche spazio e tempo.
Esempio. Uso il metro (m) per misurare lo spazio e il secondo (s) per misurare il tempo.
Poi rilevo la posizione x del punto in diversi istanti temporali t.
La tabella con le rilevazioni delle posizioni in istanti di tempo diversi è detta tabella oraria.
$$ \begin{array}{c|cc} t & x & \\ \hline 0 & 4 \\ 1 & 2 \\2 & 0 \\3 & 0 \\4 & 0 \end{array} $$
Per rappresentare il moto rettilineo disegno un diagramma cartesiano ponendo sulle ascisse il tempo t e sulle ordinate la posizione x(t).
E' detto diagramma orario.
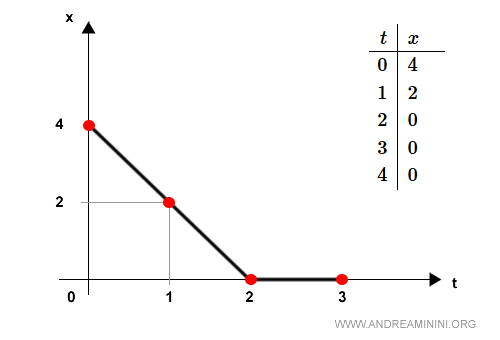
Nota. In questo esempio ho rappresentato un moto rettilineo vario perché la velocità cambia nel tempo. Il punto materiale si sposta dalla posizione x=4 alla posizione x=0 con una velocità costante fino all'istante di tempo t=2. Poi resta fermo (velocità nulla) nel punto x=0 nell'istante t=3.
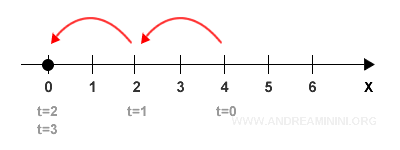
La tabella oraria mette in relazione la posizione x e il tempo t in una coppia di valori (t,x).
Spesso la relazione tra x e t può essere rappresentata anche tramite una funzione matematica x=f(t) detta legge oraria.
Nota. Non è detto che esista sempre una sola funzione matematica in grado di descrivere il moto in ogni istante di tempo. In particolar modo se si tratta di un moto vario. Quindi, un moto ha sempre una tabella oraria ma potrebbe non avere anche una legge oraria.
La legge oraria
La legge oraria del moto rettilineo è una funzione che descrive lo spostamento del punto materiale su una retta. $$ x(t) =x_0 + \Delta x $$ Dove x0 è il punto iniziale e Δx è lo spostamento.
Conoscendo la velocità media in un intervallo di tempo, posso riscrivere la legge oraria anche in questo modo
$$ x(t) = x_0 + v_m \cdot \Delta t $$
Dove Δt = t - t0 è l'intervallo di tempo usato per calcolare la velocità media e t0 è l'istante iniziale del moto..
$$ x(t) = x_0 + v_m \cdot (t-t_0) $$
Dimostrazione. La legge oraria è $$ x(t)=x_0+\Delta x $$ La velocità media è il rapporto tra lo spazio percorso Δx e il tempo impiegato Δt $$ v_m = \frac{ \Delta x}{ \Delta t} $$ Metto in evidenza lo spostamento Δx $$ \Delta x = v_m \cdot \Delta t $$ Sostituisco Δx nella legge oraria $$ x(t)=x_0+\Delta x $$ $$ x(t) = x_0 + v_m \cdot \Delta t $$ Sapendo che Δt = t - t0 ottengo la formula che volevo dimostrare $$ x(t)= x_0 + v_m \cdot (t-t_0) $$
Conoscendo la velocità istantanea v(t) del punto in ogni istante di tempo e la posizione iniziale x0 posso ricostruire la legge oraria tramite questa formula.
$$ x(t) = x_0 + \int_0^t v(t') \ dt' $$
Quest'ultima formula richiede la conoscenza dei concetti matematici di derivata e integrale.
Dimostrazione
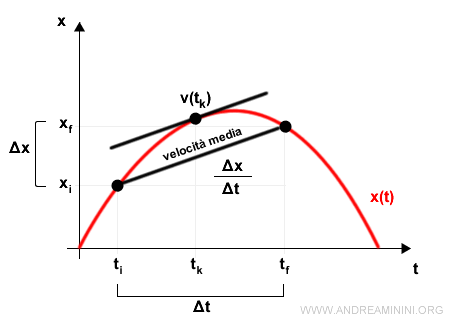
In un istante di tempo iniziale ti il punto si trova nella posizione xi.
In un istante di tempo successivo tf il punto si trova nella posizione xf.
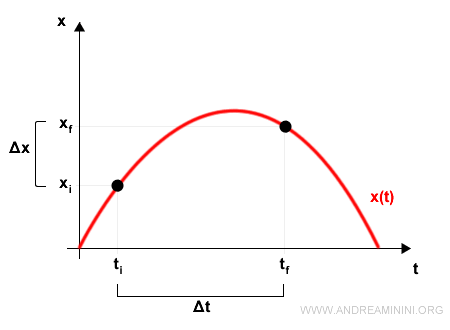
Nell'intervallo di tempo Δt=tf-ti si verifica uno spostamento del punto materiale di Δx=xf-xi sulla retta.
Una volta noto lo spostamento Δx nel tempo Δt posso calcolare la velocità media vm.
$$ v_m = \frac{ \Delta x }{ \Delta t } = \frac{x_f - x_i}{t_f - t_i} $$
La velocità media mi dice qual è la velocità costante necessaria per coprire la distanza Δx nel tempo Δt.

Purtroppo la velocità media non è utile per descrivere il moto perché si tratta di un valore medio.
Durante il moto il corpo potrebbe spostarsi a velocità diverse.
Nota. Nell'istante iniziale ti il punto materiale si sposta in avanti sull'asse x mentre nel punto finale xf si sposta indietro sull'asse x. Nel primo caso la velocità è positiva mentre nel secondo è negativa. Pertanto, a parte i casi più banali, la velocità media non indica la velocità in ogni istante del moto (velocità istantanea). Nel precedente diagramma orario la velocità media è uguale alla velocità istantanea solo nell'istante tk. In tutti gli altri istanti è diversa.
E' quindi necessario calcolare la velocità istantanea v(t), ossia la velocità del punto materiale in ogni singolo istante di tempo.
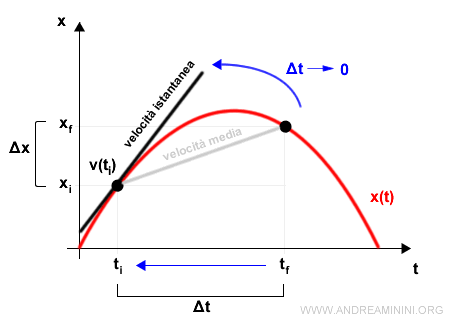
Per calcolare la velocità istantanea in un punto riduco l'intervallo temporale Δt della velocità media facendolo tendere a zero.
$$ v(t) = \lim_{ \Delta t \rightarrow 0 } \frac{\Delta x}{\Delta t} $$
In questo modo il rapporto tra l'incremento di spazio e di tempo diventa infinitesimo.
Nota. Quando si parla di velocità in fisica si intende sempre la velocità istantanea.
Dal punto di vista matematico la velocità istantanea è la derivata prima dello spostamento rispetto al tempo in un punto.
$$ v(t) = \lim_{ \Delta t \rightarrow 0 } \frac{\Delta x}{\Delta t} = \frac{dx(t)}{dt} $$
Quindi, in un diagramma orario la velocità istantanea è il coefficiente angolare della retta tangente in un punto x(t).
Il segno della velocità istantanea mi indica il verso del moto in un istante di tempo t.
- Se la velocità istantanea è positiva v(t)>0 il punto si sta muovendo nel verso della retta ossia x(t) cresce.
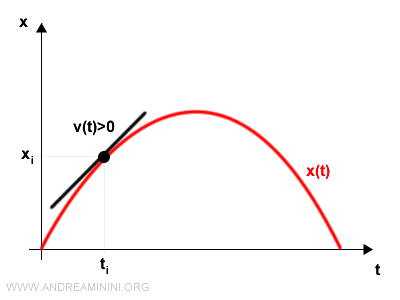
- Se la velocità istantanea è negativa v(t)<0 il punto si sta muovendo nel verso opposto rispetto alla retta ossia x(t) decresce.
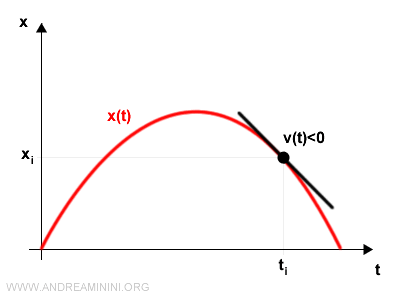
- Se la velocità istantanea è nulla v(t)=0 il punto è fermo. Non si sta muovendo. E' in uno stato di quiete.
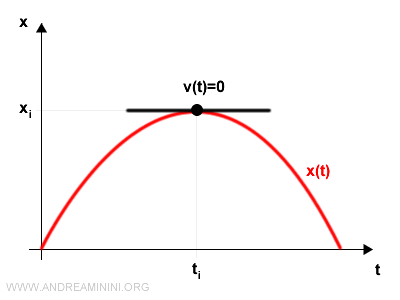
Quando la velocità v(t) è una funzione nota, posso ricavare la posizione x(t) tramite un'operazione di integrazione.
$$ x(t) = x_0 + \int_0^t v(t') \ dt' $$
Dove x0 è la posizione iniziale.
Perché? La velocità è la derivata prima dello spostamento x(t) in un istante di tempo. $$ v(t) = \frac{d \ x(t)}{dt} $$ L'operatore inverso della derivata è l'integrale. $$ x(t) = \int v(t) $$ Quindi, conoscendo la velocità v(t) e la posizione iniziale x0, posso ricostruire la legge oraria. $$ x(t) = \int_0^t v(t') \ dt' = [x(t) - x_0] + k = \Delta x + k $$ Dove k è la costante che indica la posizione iniziale x0. $$ x(t) =x_0 + \Delta x $$
L'accelerazione
L'accelerazione è la variazione di velocità v(t) nel tempo
La variazione di accelerazione media in un intervallo di tempo è il rapporto tra la variazione della velocità e la variazione del tempo.
$$ a_m = \frac{ \Delta v }{ \Delta t } $$
Anche in questo caso è utile rilevare l'accelerazione in un singolo istante di tempo, ossia l'accelerazione istantanea, facendo tendere a zero l'incremento di tempo.
$$ a = \lim_{\Delta t \rightarrow 0} \frac{ \Delta v }{ \Delta t } = \frac{ \delta v }{ \delta t } $$
Nota. Quando in fisica si parla di accelerazione senza specificare altro, si intende l'accelerazione istantanea.
A cosa serve l'accelerazione?
L'accelerazione istantanea mi consente di capire quanto sta variando la velocità in un punto in un istante di tempo.
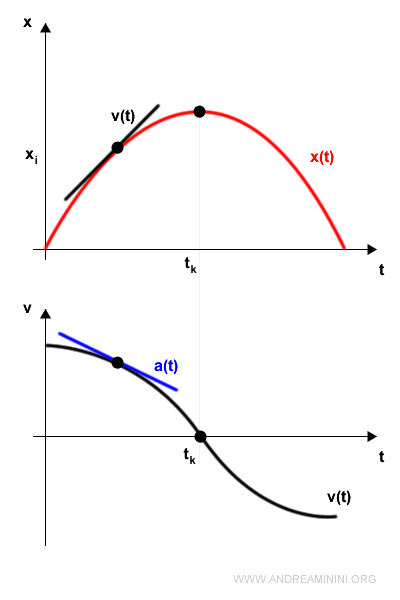
Da un punto di vista matematico, l'accelerazione istantanea è la derivata prima della velocità istantanea.
Nota. Sapendo che l'accelerazione è la derivata prima della velocità rispetto al tempo $$ a= \frac{d \ v(t)}{dt} $$ e la velocità è la derivata prima dello spostamento rispetto al tempo $$ v= \frac{d \ x(t)}{dt} $$ è facile intuire che l'accelerazione è la derivata seconda dello spostamento rispetto al tempo. $$ a= \frac{d^2 \ x(t)}{dt^2} $$
Conoscendo l'accelerazione istantanea a(t) in ogni istante di tempo e la velocità iniziale v0, posso ottenere la velocità tramite un'operazione di integrazione.
$$ v(t) = v_0 + \int_0^t a(t') \ dt' $$
E indirettamente, una volta nota la velocità, posso ricostruire la legge oraria x(t) dello spostamento.
$$ x(t) = x_0 + \int_0^t v(t') \ dt' $$
E così via.
