Moto rettilineo smorzato esponenzialmente
Il moto rettilineo smorzato esponenzialmente è caratterizzato da una velocità che si riduce in modo esponenziale nel tempo. $$ a=-kv $$
Il moto è soggetto a una forza resistente proporzionale alla velocità.
L'accelerazione è sempre contraria alla velocità.
La formula della velocità
La velocità nel tempo
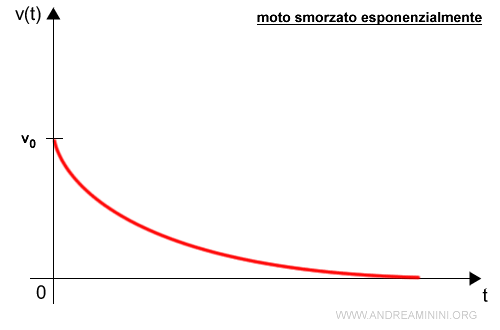
La formula della velocità del moto rettilineo smorzato esponenzialmente è $$ v(t) = v_0 e^{-kt} $$
Dove v0 è la velocità iniziale del corpo nell'istante t=0.
La velocità si riduce nel corso del tempo in modo esponenziale.
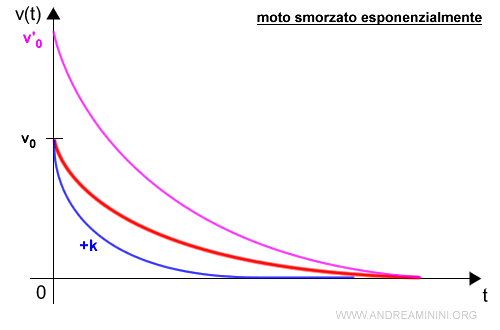
Nota. La velocità iniziale v0 può essere qualsiasi ma non deve essere nulla. Se la velocità iniziale fosse pari a zero, la velocità resterebbe nulla nel tempo. L'incremento del valore k rende lo smorzamento più rapido (e viceversa).
Dimostrazione
Sapendo che l'accelerazione è la derivata prima della velocità
$$ a=-kv $$
$$ \frac{δv}{δt}=-kv $$
$$ \frac{δv}{v}=-kδt $$
Metto sotto integrale entrambi i membri
$$ \int_{v_0}^v \frac{δv}{v}= \int_{0}^t -kδt $$
$$ log \frac{v}{v_0} = -kt $$
$$ v = v_0 \cdot e^{-kt} $$
La velocità nello spazio
La variazione della velocità rispetto alla posizione del punto nello spazio
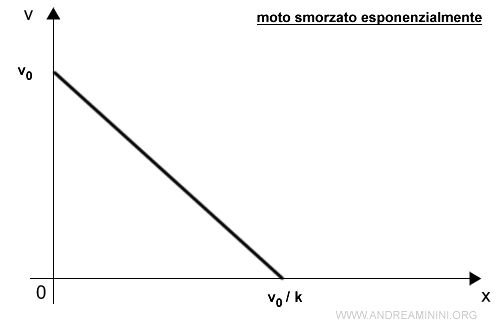
Nello spazio la velocità v(x) si riduce in modo lineare decrescente $$ v(x) = v_0 -kx $$
La velocità v(x) si azzera nella posizione x=v0/k dove il punto si ferma.
Dimostrazione
L'accelerazione del corpo nel tempo è
$$ a = \frac{dv}{dt} $$
Moltiplico entrambi i membri per dx
$$ a = \frac{dv}{dt} \cdot \frac{dx}{dx} $$
$$ a = \frac{dv}{dx} \cdot \frac{dx}{dt} $$
Il rapporto dx/dt è la velocità v
$$ a = \frac{dv}{dx} \cdot v $$
Nel moto smorzato esponenzialmente l'accelerazione è a=-kv
$$ -kv = \frac{dv}{dx} \cdot v $$
Semplifico eliminando la v nel membro di destra e di sinistra
$$ -k = \frac{dv}{dx} $$
Sposto dx a sinistra
$$ -k \cdot dx = dv $$
Quindi integro
$$ \int_0^x -k \cdot dx = \int_{v_0}^v dv $$
$$ -k \int_0^x dx = \int_{v_0}^v dv $$
$$ -k \cdot x = v(x)-v_0 $$
E ottengo la formula
$$ v(x) = v_0-k \cdot x $$
La legge oraria
La legge oraria del moto rettilineo smorzato esponenzialmente è $$ x = x_0 + \frac{v_0}{k}(1-e^{-kt}) $$
Dove x0 è la posizione iniziale, v0 è la velocità iniziale e k è un parametro che dipende dalla forma, dalla massa e dalla densità del corpo in moto.
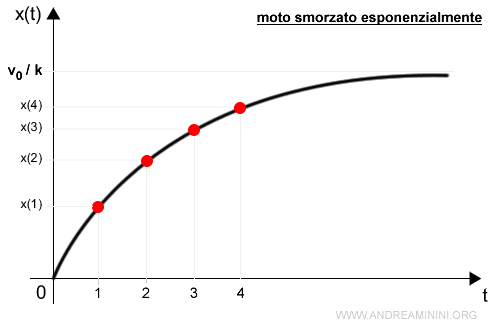
Nota. Poiché la velocità si riduce nel tempo, il moto del punto uniforme rallenta in modo esponenziale fino a fermarsi del tutto nella posizione v0/k.
Il punto tende asintoticamente alla posizione v0/k.
Nella posizione x=v0/k la velocità si annulla e il punto si ferma.
Dimostrazione
La legge del moto orario si ottiene integrando la velocità v(t) rispetto al tempo
$$ x(t) = x_0 + \int_0^t v(t) \: dt $$
Sapendo che v(t)=v0e-kt
$$ = x_0 + \int_0^t v_0 e^{-kt} \: dt $$
$$ = x_0 + v_0 \int_0^t e^{-kt} \: dt $$
L'integrale di ∫e-kt rispetto alla variabile t è (e-kt)/-k
Quindi, applico il teorema fondamentale dell'integrazione.
$$ = x_0 + v_0 \cdot [ \frac{e^{-kt}}{-k} ]^t_0 $$
$$ = x_0 + v_0 \cdot ( \frac{e^{-kt}}{-k} - \frac{e^{-k·0}}{-k} ) $$
$$ = x_0 + v_0 \cdot ( \frac{e^{-kt}}{-k} - \frac{1}{-k} ) $$
$$ = x_0 - \frac{v_0}{k} \cdot ( e^{-kt} - 1 ) $$
$$ = x_0 + \frac{v_0}{k} \cdot ( 1 - e^{-kt} ) $$
La costante tempo
Nel moto smorzato esponenzialmente il valore k determina la rapidità o meno della decrescita.
- Se k è grande, la decrescita è rapida
- Se k è piccolo, la decrescita è lenta
Per analizzare questo fenomeno studio la variazione della funzione e-kt rispetto a una variazione di tempo τ.
$$ \frac{e^{-k(t+τ)}}{e^{-kt}} $$
Svolgo le semplificazioni algebriche
$$ = e^{-kτ} $$
Ponendo τ=1/k ottengo
$$ = e^{-k\frac{1}{k}} $$
$$ = e^{-1} $$
Con questo valore τ la funzione diventa una funzione esponenziale con e=2.72 ed è facile da misurare.
La costante τ=1/t è detta costante tempo e si misura in secondi.
In questo caso la velocità si smorza quasi completamente dopo 5τ
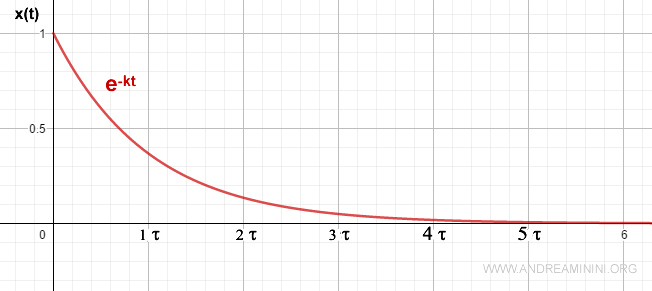
Contemporaneamente il moto si arresta a 1 dopo 5τ
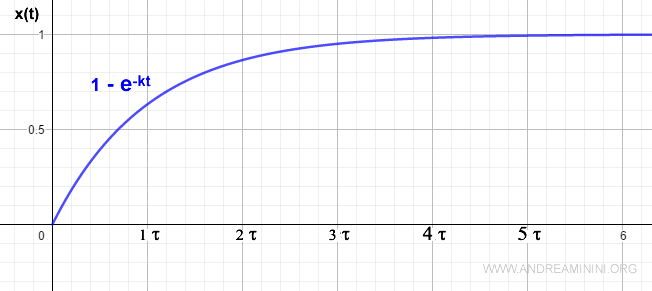
Nota. E' evidente che il valore della costante tempo sia correlato inversamente al valore di k. Se k è grande, τ è piccolo e viceversa.
E così via.
