Il moto uniformemente accelerato

Il moto rettilineo è uniformemente accelerato se l'accelerazione è costante e diversa da zero.

Le principali cararatteristiche del moto rettilineo uniformemente accelerato

Nel moto rettilineo uniformemente accelerato l'accelerazione è una costante diversa da zero.

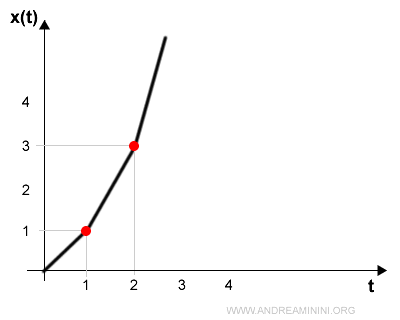
Quindi, la velocità è una funzione lineare rispetto al tempo (t) mentre il diagramma orario è una parabola.

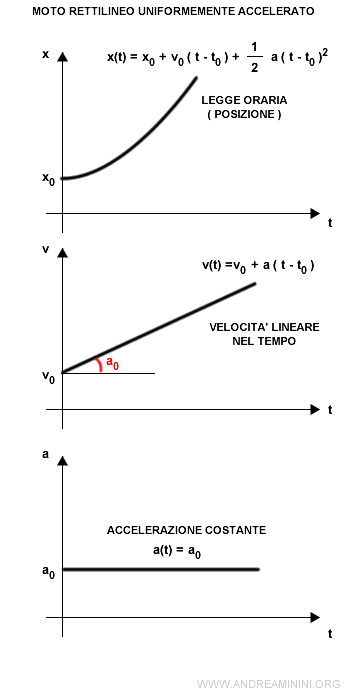
Le formule del moto rettilineo uniformemente accelerato sono le seguenti

Accelerazione

$$a(t) = a_0$$

Velocità

$$v(t) = v_0 + a(t-t_0)$$

Posizione (legge oraria)

$$x(t) = x_0 + v_0 (t-t_0) + \frac{1}{2} a(t-t_0)^2$$

Dove t₀ è l'istante iniziale, x₀ è la posizione iniziale, v₀ è la velocità iniziale, a₀ è l'accelerazione iniziale.

Nota. Nel caso semplificato in cui t₀ = 0 l'accelerazione diventa $$v(t) = v_0 + a \cdot t$$ mentre la legge oraria si riduce a $$x(t) = x_0 + v \cdot t + \frac{1}{2} a \cdot t^2$$

L'accelerazione

Nel moto uniformemente accelerato l'accelerazione è costante $$a(t) = a_0$$

E' molto semplice e non c'è molto da aggiungere.

Se l'accelerazione è positiva si parla di moto uniformemente accelerato.

Viceversa, se l'accelerazione è negativa si parla di moto ritardato.

La velocità

Nel moto uniformemente accelerato la velocità è $$v(t) = a_0 (t-t_0) + v_0$$ oppure in modo equivalente $$v(t) = v_0 + \int_{t_0}^{t} a_0 \: dt$$

Si tratta di una retta.

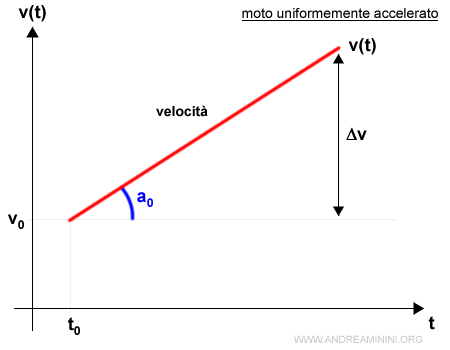
Se la retta ha inclinazione positiva la velocità aumenta nel tempo.

Viceversa, se la retta ha inclinazione negativa la velocità si riduce nel tempo.

Dimostrazione

L'accelerazione è uguale alla derivata della velocità rispetto al tempo.

$$a(t) = \frac{d \: v(t)}{dt}$$

Nel moto uniformemente accelerato l'accelerazione è una costante a₀

$$\frac{d \: v}{dt} = a_0$$

Applico la tecnica della separazione delle variabili

$$d \: v = a_0 \: dt$$

Poi integro entrambi i membri.

$$\int_{v_0}^{v(t)} d \: v = \int_{t_0}^t a_0 \: dt$$

Nota. Il membro di sinistra l'ho integrato per la variabile velocità v(t) mentre quello di destra l'ho integrato per il tempo perché la variabile di integrazione è diversa.

Risolvo l'integrale di sinistra con il teorema fondamentale dell'integrazione.

$$v(t)-v_0 = \int_{t_0}^t a_0 \: dt$$

Nell'integrale di destra sposto la costante a0 fuori dall'integrale e integro dt con il teorema fondamentale dell'integrazione.

$$v(t)-v_0 = a_0 \cdot \int_{t_0}^t \: dt$$

$$v(t)-v_0 = a_0 (t-t_0)$$

Metto in evidenza v(t) e ottengo la formula della velocità nel moto rettilineo uniforme.

$$v(t) = a_0 (t-t_0) + v_0$$

La velocità in funzione della posizione $$v^2 = v_0^2 + 2a (x-x_0)$$ Per una spiegazione sulla formula.

La legge oraria

Nel moto uniformemente accelerato la posizione del punto nello spazio è $$x(t) = x_0 + v_0(t-t_0) + \frac{1}{2} a \cdot (t-t_0)^2$$

Graficamente è una parabola.

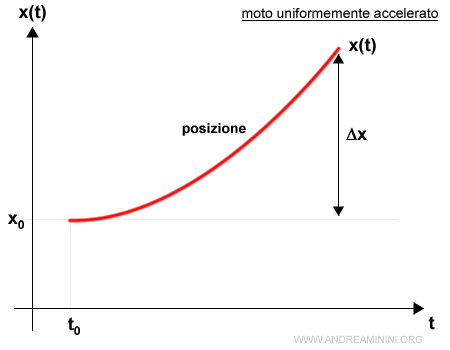
La parabola è rivolta verso l'alto se l'accelerazione è positiva. Verso il basso se è negativa.

Dimostrazione

La posizione x(t) del punto materiale è in funzione del punto iniziale x₀ e della velocità v(t).

La formula della legge oraria è la seguente:

$$x(t) = x_0 + \int_{t_0}^{t} v(t) dt$$

Sostituisco v(t) con la formula dell'accelerazione.

$$x(t) = x_0 + \int_{t_0}^{t} [v_0 + a \cdot (t-t_0) ] \ dt$$

Nota. Nel moto uniformemente accelerato la velocità del punto materiale è lineare e dipende dal tempo. $$v(t) = v_0 + \int_{t_0}^{t} a(t) \: dt$$ $$v(t) = v_0 + a \cdot t - a \cdot t_0$$ $$v(t) = v_0 + a \cdot (t-t_0)$$

Separo i due integrali

$$x(t) = x_0 + \int_{t_0}^{t} v_0 \ dt + \int_{t_0}^{t} a \cdot (t-t_0) \ dt$$

Quindi svolgo i due integrali

$$x(t) = x_0 + v_0(t-t_0) + \frac{1}{2} a \cdot (t-t_0)^2$$

Nota. Se l'istante iniziale è uguale a zero t₀=0 $$x(t) = x_0 + v_0 t + \frac{1}{2} a t^2$$

Ho così ottenuto la posizione x(t) del punto nello spazio in un moto rettilineo uniformemente accelerato in funzione della posizione iniziale (x₀), della velocità (v) e dell'accelerazione (a).

La velocità è in funzione lineare del tempo.

L'accelerazione è invece in funzione quadratica del tempo.

E così via.