Il moto rettilineo uniforme
Nel moto rettilineo uniforme il punto materiale si sposta su una retta con velocità costante
Le principali cararatteristiche del moto rettilineo uniforme
Nel moto rettilineo uniforme un punto materiale si sposta su una retta con coefficiente angolare pari alla velocità costante v0.
Essendo la velocità costante, l'accelerazione del moto è nulla
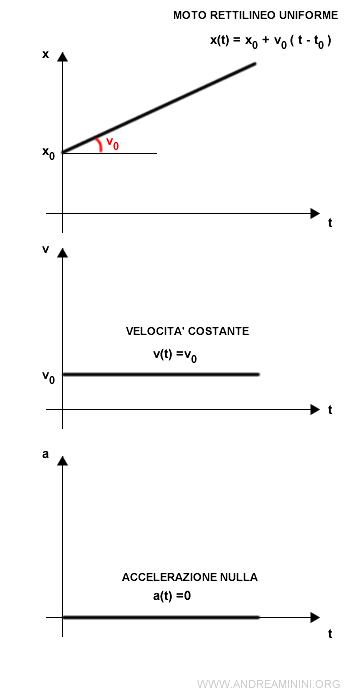
Le formule del moto rettilineo uniforme sono le seguenti
Accelerazione
$$ a(t) = 0 $$
Velocità
$$ v(t) = v_0 $$
Posizione (legge oraria)
$$ x(t) = x_0 + v(t-t_0) $$
Dove v0 è la velocità iniziale, x0 è la posizione iniziale, t0 è l'istante iniziale, t è il tempo.
L'accelerazione
Nel moto rettilineo l'accelerazione è uguale alla derivata della velocità ed è nulla perché la velocità è costante $$ a(t) = \frac{d \: v(t)}{d \: t} = 0 $$
Dimostrazione
L'accelerazione è la derivata prima della velocità
$$ a(t) = \frac{d \: v(t)}{d \: t} $$
Nel moto rettilineo uniforme la velocità è costante v0.
La derivata di una costante è sempre uguale a zero.
$$ a(t) = \frac{d \: v_0}{d \: t} = 0 $$
Pertanto, nel moto rettilineo uniforme l'accelerazione è nulla.
$$ a(t) = 0 $$
La velocità
Nel moto rettilineo uniforme la velocità è costante ed è uguale alla derivata della posizione $$ v(t) = v_0 = \frac{d \: x(t)}{d \: t} $$
La velocità nel moto è rettilineo uniforme è rappresentabile sul diagramma cartesiano con una retta parallela all'ascisse.
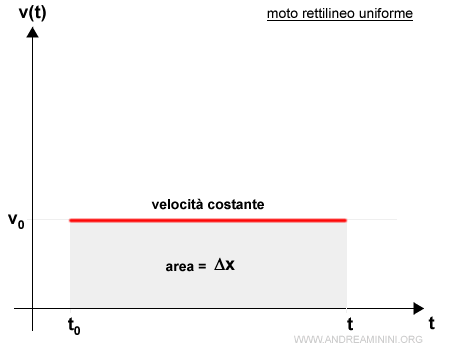
L'area compresa tra la retta delle velocità v0 e l'ascisse è uguale allo spostamento del punto nello spazio Δx nell'intervallo di tempo t0-t.
Dimostrazione
L'accelerazione è la derivata della velocità.
Quindi, posso calcolare la velocità tramite l'integrale dell'accelerazione.
$$ v(t) = \int a(t) \ dt $$
Nel moto rettilineo uniforme l'accelerazione istantanea è sempre nulla a(t)=0
$$ v(t) = \int 0 \ dt $$
L'integrale di 0 è una costante v0 ossia la velocità iniziale.
$$ v(t) = \int 0 \ dt = v_0 $$
Pertanto, in qualsiasi momento del moto la velocità istantanea v(t) è uguale alla velocità iniziale v0.
La legge oraria
La legge oraria del moto rettilineo è una funzione che determina la posizione del punto materiale in funzione del tempo. Se il moto è rettilineo uniforme la formula è $$ x(t) = x_0 + v_0(t-t_0) $$ o in modo equivalente $$ x(t) = x_0 + \int_{t_0}^t v_0 \: dt $$
Nel caso semplificato in cui l'istante iniziale è t0=0 diventa
$$ x(t) = x_0 + v_0 \cdot t $$
Dal punto di vista grafico la legge oraria del moto rettilineo uniforme è una retta con angolazione pari alla velocità.
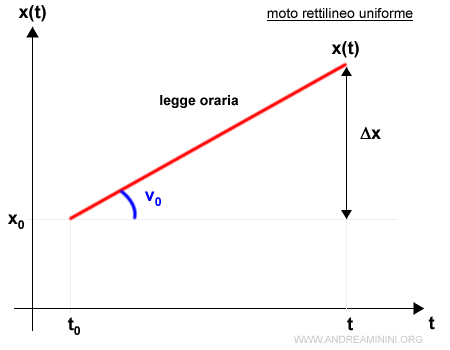
Lo spazio è una funzione lineare del tempo.
Pertanto, il diagramma orario si presenta come una retta con coefficiente angolari pari alla velocità.
Dimostrazione
La velocità è la derivata prima della legge oraria ossia dello spostamento
$$ v(t) = \frac{d \: x(t)}{d \: t} $$
Sposto il differenziale dt a sinistra
$$ dt \: v(t) = d \: x $$
Poi integro entrambi i membri per le rispettive variabili
$$ \int_{t_0}^t v(t) \:dt = \int_{x_0}^{x(t)} dx $$
Essendo il moto rettilineo uniforme la velocità è una costante v0 e posso farla uscire dall'integrale
$$ \int_{t_0}^t v_0 \:dt = \int_{x_0}^{x(t)} dx $$
$$ v_0 \int_{t_0}^t dt = \int_{x_0}^{x(t)} dx $$
Svolgo i due integrali con il teorema fondamentale dell'integrazione
$$ v_0 ( t - t_0) = x(t) - x_0 $$
Metto in evidenza la legge oraria x(t)
$$ x(t) = x_0 + v_0 ( t - t_0) $$
Ho ottenuto la formula della legge oraria del moto rettilineo uniforme
E così via
