Un insieme connesso è contenuto interamente in una componente connessa
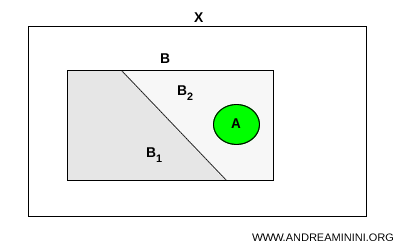
Dati due sottoinsiemi \( A \) e \( B \) di uno spazio topologico \( X \), con \( A \) connesso e \( A \subset B \), se \( B \) ammette una separazione in due insiemi \( B_1 \) e \( B_2 \) in \( X \), allora \( A \) è contenuto interamente in una sola delle due parti: $$ A \subset B_1 \quad \text{oppure} \quad A \subset B_2 $$
Un insieme connesso non può attraversare una separazione.
Se è contenuto in un insieme che si divide in due parti disgiunte, allora deve essere contenuto completamente in una sola di esse.
In altre parole, un insieme connesso è come un pezzo unico di corda dentro una busta. Se la busta viene divisa in due parti separate e la corda è integra, allora deve trovarsi tutta in una sola parte, altrimenti sarebbe spezzata. La connessione impedisce di “stare a cavallo” di una separazione, così come una corda integra non può essere divisa senza rompersi.
Un esempio pratico
Considero lo spazio topologico:
$$ X = \mathbb{R} $$
e un sottoinsieme di \( X \):
$$ B = (-3,4) $$
Questo insieme può essere separato nei due sottoinsiemi:
$$ B_1 = (-3,0) $$
$$ B_2 = (0,4) $$
I due sottoinsiemi sono disgiunti:
$$ B_1 \cap B_2 = \varnothing $$
e la loro unione ricopre \( B \):
$$ B_1 \cup B_2 = B $$
Inoltre, \( B_1 \) e \( B_2 \) sono aperti nella topologia indotta su \( B \).
Quindi formano una separazione di \( B \) in \( X \).
Ora considero un insieme connesso contenuto in \( B \):
$$ A = (1,2) $$
Poiché $ A \subset B_2 $ l’insieme \( A \) è contenuto interamente in una sola delle due parti della separazione.
Nota. Se prendo $ A = (-1,1) $ allora risulta: $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ Ma questo è impossibile, perché \( B_1 \) e \( B_2 \) formano una separazione di \( B \). Un insieme connesso contenuto in \( B \) non può essere diviso tra i due insiemi della separazione. Infatti, se ciò accadesse, \( A \) sarebbe separato, in contraddizione con il fatto che l’intervallo \( (-1,1) \) è connesso. Il punto non è che \( (-1,1) \) non sia connesso... Il punto è che non può essere contenuto in \( B \) quando \( B \) è separato in quel modo.
Dimostrazione
Ipotesi
Siano \( A \) e \( B \) sottoinsiemi di uno spazio topologico \( X \).
$$ A \subset X \quad e \quad B \subset X $$
Si supponga che:
- \( A \) è connesso
- \( A \subset B \)
- \( B_1 \) e \( B_2 \) formano una separazione di \( B \) in \( X \)
Tesi
Allora \( A \) è un sottoinsieme di \( B_1 \) oppure di \( B_2 \)
$$ A \subset B_1 \quad \text{oppure} \quad A \subset B_2 $$
Dimostrazione
Per ipotesi, \( B_1 \) e \( B_2 \) formano una separazione di \( B \) in \( X \). Quindi valgono le seguenti proprietà:
- \( B_1 \cap B_2 = \varnothing \) ossia \( B_1 \) e \( B_2 \) sono disgiunti
- \( B = B_1 \cup B_2 \) ossia la loro unione copre interamente \( B \)
- \( B_1 \) e \( B_2 \) sono aperti nella topologia indotta su \( B \).
Suppongo per assurdo che non valga né \( A \subset B_1 \) né \( A \subset B_2 \) ossia che \( A \) non sia interamente contenuto in \( B_1 \) o in \( B_2 \).
$$ A \cap B_1 \neq \varnothing \qquad \text{e} \qquad A \cap B_2 \neq \varnothing $$
Poiché \( A \subset B \), si ha:
$$ A = A \cap B = A \cap (B_1 \cup B_2) = (A \cap B_1) \cup (A \cap B_2) $$
Poiché \( B_1 \) e \( B_2 \) sono disgiunti, allora anche \( A \cap B_1) e \( A \cap B_2) sono disgiunti.
Pertanto, gli insiemi \( A \cap B_1 \) e \( A \cap B_2 \) sono disgiunti, non vuoti e aperti nella topologia indotta su \( A \). Quindi, formano una separazione di \( A \) in \( X \).
Ma questo è impossibile, poiché per ipotesi iniziale \( A \) è connesso.
Segue che l’assunzione iniziale è falsa, e quindi è vero il contrario:
$$ A \subset B_1 \quad \text{oppure} \quad A \subset B_2 $$
Questo conclude la dimostrazione.
E così via.
