Separazione di un sottospazio tramite insiemi aperti
Sia \( A \) un sottoinsieme di \( X \). Gli insiemi aperti \( U \) e \( V \) di \( X \) si dicono una separazione di \( A \) se soddisfano le seguenti condizioni:
- Ricoprono \( A \) \[ A \subseteq U \cup V \]
- Ciascuno contiene una parte di \( A \) \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
- Non si sovrappongono dentro \( A \) \[ U \cap V \cap A = \varnothing \]
In altre parole, l’insieme \( A \) viene diviso in due parti disgiunte e separate: una parte contenuta in \( U \) e l’altra contenuta in \( V \).
Questa è un’altra modalità per definire la separazione di un insieme tramite la topologia.
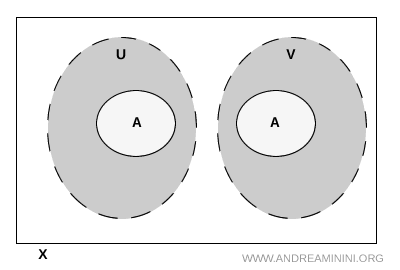
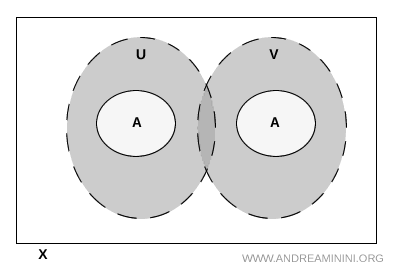
Nota. Non è necessario che \( U \) e \( V \) siano disgiunti in tutto lo spazio \( X \). Possono anche sovrapporsi al di fuori di \( A \). L’importante è che non si sovrappongano quando vengono intersecati con \( A \).
Un esempio pratico
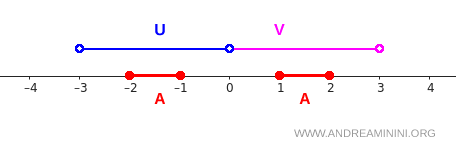
Considero lo spazio topologico \(X = \mathbb{R} \) con la topologia standard e un insieme \( A \) formato da due parti separate.
$$ A = [-2,-1] \cup [1,2] $$
Definisco due insiemi aperti aperti di (X):
$$ U = (-3,0) $$
$$ V = (0,3) $$
Ecco la rappresentazione grafica degli intervalli:
Poi controllo le condizioni della definizione.
La parte \( [-2,-1] \) di \( A \) sta dentro \(U \)
La parte \( [ 1,2] \) di \( A \) sta dentro \( V \)
Quindi, l'insieme \( A \) è un sottoinsieme dell'unione \( U \cup V \)
$$ A \subseteq U \cup V $$
Entrambi gli insiemi aperti includono una parte di \( A \).
$$ U \cap A = [-2,-1] \neq \varnothing $$
$$ V \cap A = [1,2] \neq \varnothing $$
Inoltre, i due insiemi aperti non si sovrappongono dentro \( A \)
$$ U \cap V \cap A = \varnothing $$
Pertanto, posso affermare certamente che gli insiemi aperti \( U \) e \( V \) formano una separazione dell'insieme \( A \) nello spazio \( X \).
E così via.
