Criterio di connessione tramite intersezione non vuota
Data una collezione \( C_1, C_2, \dots, C_n \subset X \) di insiemi connessi di \( X \) che si intersecano in almeno un punto \[
\bigcap_{i=1}^n C_i \neq \varnothing \] la loro unione \( \bigcup_{i=1}^n C_i \) è un insieme connesso
In altre parole, se due o più insiemi connessi di \( X \) hanno almeno un punto in comune, allora la loro unione è ancora un insieme connesso.
Questo teorema della connessione richiede esplicitamente che l’intersezione comune tra tutti gli insiemi non sia vuota.
Nota. L’ipotesi di intersezione non nulla \( \bigcap_{i=1}^n C_i \neq \varnothing \) degli insiemi connessi è una condizione sufficiente per garantire che la loro unione \( \bigcup_{i=1}^n C_i \) sia connessa, ma non è una condizione necessaria. Infatti l’unione degli insiemi connessi potrebbe essere connessa anche quando non esiste un punto comune a tutti gli insiemi. Ad esempio, in caso di intersezione a catena.
Un esempio pratico
Considero nello spazio \( \mathbb{R}^2 \) i seguenti insiemi:
- \( C_1 \): il segmento orizzontale da \( (-1,0) \) a \( (1,0) \)
- \( C_2 \): il segmento verticale da \( (0,-1) \) a \( (0,1) \)
- \( C_3 \): il segmento obliquo che unisce \( (-1,-1) \) a \( (1,1) \)
Tutti e tre gli insiemi sono connessi.
Inoltre, tutti contengono il punto ( (0,0) ). Infatti:
\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]
Quindi l’intersezione comune non è vuota:
\[ \bigcap_{i=1}^3 C_i = {(0,0)} \]
Di conseguenza, per il teorema sulla connessione, la loro unione è un insieme connesso.
\[ C_1 \cup C_2 \cup C_3 \]
I tre segmenti si incontrano tutti nello stesso punto centrale. Questo garantisce la connessione dell’insieme.
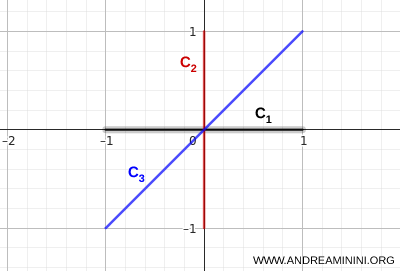
Da qualunque punto di un segmento è possibile raggiungere qualunque altro punto passando sempre attraverso punti appartenenti all’unione.
Nota. Esistono altri criteri di connessione che non richiedono un punto comune a tutti gli insiemi \( C_i \), cioè non richiedono che \( \bigcap_i C_i \neq \varnothing \). Ad esempio, se gli insiemi \( C_i \) sono connessi e si intersecano a catena, \( C_i \cap C_{i+1}\neq\varnothing \), allora l’unione \( \bigcup_i C_i \) è connessa anche se \( \bigcap_i C_i = \varnothing \). Tuttavia, la condizione dell'intersezione a catena non è necessaria, perché l’unione può essere connessa anche quando qualche coppia consecutiva è disgiunta, purché esistano altri insiemi della famiglia che fungono da collegamento. Ad esempio, considero tre segmenti che formano un triangolo. L'intersezione di questi segmenti è un insieme vuoto \( \bigcap_i C_i = \varnothing \), non c'è un punto in comune, ma l'unione degli insiemi è connessa.
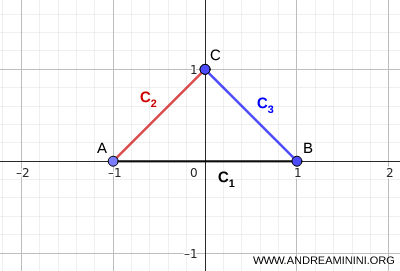
Questo esempio mostra chiaramente che l’intersezione a catena è sufficiente per garantire la connessione dell’unione.
Dimostrazione
Considero uno spazio topologico \( X \) e una famiglia \({C_i}_{i \in I} \) di insiemi connessi dj \( X \) che si intersecano almeno in un punto in comune
\[ \bigcap_{i \in I} C_i \neq \varnothing \]
Suppongo per assurdo che l'unione $ C $ non sia connessa
\[ C = \bigcup_{i \in I} C_i \]
Se $ C $ non è connesso, allora esistono due insiemi aperti \( U \) e \( V \) che formano una separazione di \( C \), cioè:
- \( U \cap C \neq \varnothing \)
- \( V \cap C \neq \varnothing \)
- \( (U \cap C) \cap (V \cap C) = \varnothing \)
- \( C = (U \cap C) \cup (V \cap C) \)
Poiché per ipotesi l'intersezione degli insiemi $ C_i $ non è nulla
\[ \bigcap_{i \in I} C_i \neq \varnothing \]
deve esistere un punto in comune $ x $ in $ C $ tra tutti gli insiemi $ C_i $
\[ x \in \bigcap_{i \in I} C_i \]
Questo punto in comune potrebbe stare in $ x \in U $ oppure in $ x \in V $ ma non entrambi poiché formano una separazione di $ C $. Ad esempio, in $ U $ ma non in $ V $ o viceversa.
\[ x \in U \quad \text{e} \quad x \notin V \]
Poiché ogni insieme \( C_i \subset C \) appartiene a $ C $, posso scrivere:
\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]
Sapendo che \( C_i \cap U \) e \( C_i \cap V \) sono aperti in \( C_i \), sono disgiunti e la loro unione è tutto \( C_i \), poiché \( C_i \) è connesso per ipotesi iniziale, uno dei due insiemi $ U $ o $ V $ deve essere vuoto.
Dunque, \( C_i \) deve essere un sottoinsieme di $ U $ oppure di $ V $
\[ C_i \subset U \quad \text{oppure} \quad C_i \subset V \]
Se \( x \in C_i \) e \( x \in U \), allora non può essere \( C_i \subset V \).
Segue che:
\[ C_i \subset U \quad \text{per ogni } i \in I \]
Da quanto sopra ottengo che l'unione $ C $ è un sottoinsieme di $ U $
\[ \bigcup_{i \in I} C_i \subset U \]
Ma questo è impossibile, perché \( V \cap C \neq \varnothing \) per l'ipotesi di separazione.
La contraddizione mostra che l’ipotesi iniziale è falsa. Quindi, è vero il suo contrario, ossia che l’unione \( \bigcup_{i \in I} C_i \) è un insieme connesso.
E così via.
