Caratterizzazione degli insiemi sconnessi tramite gli aperti dello spazio

In altre parole, ogni volta che un insieme \( A \) è sconnesso, posso sempre trovare intorno due insiemi aperti di \( X \), disgiunti e non vuoti, che raccolgono le due parti di \( A \)

E viceversa, se posso farlo, allora l’insieme è sconnesso.

A cosa serve?

Questo teorema permette di valutare se un sottoinsieme \( A \) è sconnesso nello spazio topologico \( X \) che lo contiene tramite gli insiemi aperti dello spazio stesso \(X\).

Un esempio pratico

Considero l'insieme \( A \) nello spazio topologico \( \mathbb{R} \)

$$ A = [0,1] \cup [2,3] \in X = \mathbb{R}  $$

Questo insieme è ovviamente sconnesso perché ci sono due parti separate:

• l'intervallo \( [0,1] \)
• l'intervallo \( [2,3] \)

Il teorema dice che devono esistere due insiemi aperti di \( X \) che separano \( A \). In questo caso \( X = \mathbb{R} \).

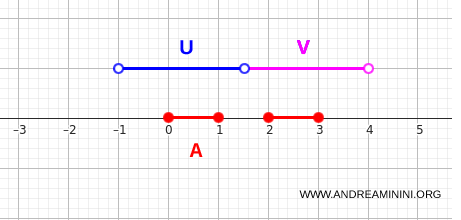
Scelgo due insiemi aperti di \( \mathbb{R} \) che contengono almeno un elemento di \( A \), ad esempio:

• $ U = (-1,1.5) $
• $ V = (1.5,4) $

Questi sono due insiemi aperti nella retta reale.

I due insiemi intersecano \( A \) e l'intersezione non è nulla come richiesto dal teorema.

$$ U \cap A = [0,1]  \neq \varnothing  $$

$$ V \cap A = [2,3]  \neq \varnothing $$

L'intersezione delle intersezioni è nulla, come richiesto dal teorema, perché \( U \) e \( V \) non si sovrappongono su nessun punto di \( A \)

$$ (U \cap V) \cap A = \varnothing $$

Quindi, questi due insiemi aperti di \( X \) tagliano \( A \) esattamente in due pezzi sconnessi.

Pertanto, l'insieme \( A \) è sconnesso in \(  \mathbb{R} \).

Esempio 2

Considero un insieme contenente due punti sulla retta dei numeri reali \( \mathbb{R} \).

$$ A = \{ 1, 3 \} \in X = \mathbb{R} $$

Questo insieme è sconnesso, perché i due punti non sono collegati da alcun tratto continuo: sono completamente separati.

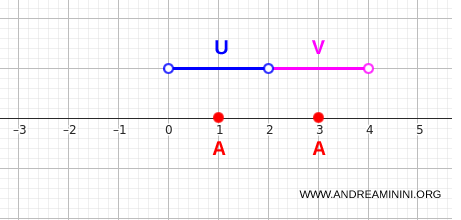
Per verificarlo tramite la caratterizzazione con gli aperti dello spazio, scelgo due intervalli aperti di \( \mathbb{R} \):

$$ U = (0,2) $$

$$ V = (2,4) $$

Ognuno contiene almeno un elemento di \( A \), perché le intersezioni non sono vuote:

$$ U \cap A = \{ 1 \} $$

$$ V \cap A = \{ 3 \} $$

Inoltre, le due parti di \(A\) catturate da \(U\) e \(V\) non si sovrappongono:

$$ U \cap V \cap A = \varnothing $$

Queste condizioni mostrano che \(A\) può essere diviso in due sottoinsiemi non vuoti, disgiunti e aperti nella topologia di sottospazio. 

Pertanto, l'insieme \( A \) è sconnesso in \( \mathbb{R} \).

Esempio 3

Considero il piano senza l'asse $ x $

$$ A = {(x,y) \in \mathbb{R}^2 : y>0} \cup {(x,y)\in\mathbb{R}^2 : y<0} $$

Anche questo è sconnesso.

Gli insiemi aperti che lo separano sono:

$$ U = {(x,y) : y> -1} $$

$$ V = {(x,y) : y< 1} $$

Questi due insiemi aperti intersecano \( A \):

• \( U \cap A \) prende tutto il semipiano superiore
• \( V \cap A \) prende tutto il semipiano inferiore

Non c’è nessun punto di \( A \) dove i due pezzi si toccano

$$ (U \cap V) \cap A = \varnothing $$

Quindi, l'insieme \( A \) è sconnesso.

Dimostrazione

La dimostrazione va divisa in due parti:

A] Se esistono tali aperti, allora \(A\) è sconnesso

Supponiamo che esistano \(U\) e \(V\) aperti in \(X\) che soddisfano le quattro condizioni.

Considero le intersezioni:

\[ P = U \cap A, \qquad Q = V \cap A \]

Per ipotesi:

• \(P\) e \(Q\) sono non vuoti
• \(P\) e \(Q\) sono aperti nella topologia di sottospazio
• \(P \cap Q = (U \cap V) \cap A = \varnothing\)
• \(P \cup Q = A\) perché \(A \subset U \cup V\)

La coppia \(P, Q\) è quindi una separazione di \(A\).

Dunque \(A\) è sconnesso.

B] Se \(A\) è sconnesso, allora esistono tali aperti.

Ora assumiamo che \(A\) sia sconnesso.

Per definizione, esistono due insiemi non vuoti

$$ P, Q \subset A $$

tali che:

• sono aperti in \(A\)
• sono disgiunti
• soddisfano \(P \cup Q = A\)

Poiché \(P\) è aperto in \(A\), esiste un aperto \(U\) di \(X\) tale che

$$ P = U \cap A $$

Analogamente, esiste un aperto \(V\) di \(X\) tale che

$$ Q = V \cap A $$

Verifichiamo ora le quattro condizioni:

• Da \(A = (U \cap A) \cup (V \cap A)\) segue \(A \subset U \cup V\)
• \(U \cap A = P \neq \varnothing\)
• \(V \cap A = Q \neq \varnothing\)
• \((U \cap V) \cap A = (U \cap A) \cap (V \cap A) = P \cap Q = \varnothing\)

Tutte le condizioni sono soddisfatte.

Dunque esistono aperti di \(X\) che separano \(A\).

C] Conclusione

Questo dimostra che un insieme \( A \) è sconnesso se e solo se può essere coperto da due aperti che lo tagliano in due parti non vuote e disgiunte.

E così via.