Spazio topologico connesso

Definizione tramite gli insiemi aperti

In altre parole, uno spazio è topologicamente connesso quando non può essere diviso in due parti aperte, disgiunte e non vuote, la cui unione costituisca tutto lo spazio.

Se esiste una tale coppia di insiemi esiste, allora lo spazio si dice disconnesso, e la coppia ( (U, V) ) si chiama separazione di ( X ).

Nota. Questa è la definizione di connessione topologica tramite l'utilizzo degli insiemi aperti. Come si vedrà, questa definizione si distingue da quella "per cammino" o "per archi". Le due definizioni di connessione non coincidono sempre.

Un esempio pratico

Considero l’insieme $ X $ composto da tre elementi

$$ X = {a, b, c} $$

Su $ X $ definisco due topologie diverse:

• Topologia A
  Gli insiemi aperti sono: $$ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $$
• Topologia B
  Gli insiemi aperti sono: $$ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $$

Quale dei due è connesso?

Secondo la definizione, uno spazio topologico ( X ) è connesso se non esistono due insiemi aperti non vuoti, disgiunti, la cui unione sia tutto ( X ).

Se una tale coppia esiste, si chiama separazione di ( X ) e lo spazio si dice disconnesso.

1] Topologia A

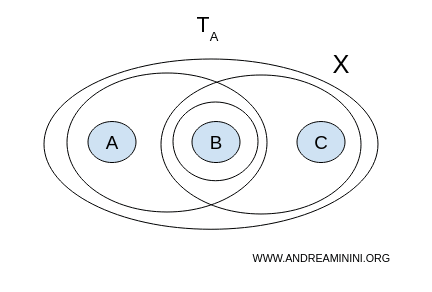
Cerco una separazione $ (U, V) $ con la topologia $ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $ ossia una combinazione di due insiemi aperti, non vuoti e disgiunti che coprano interamente lo spazio $ X $

• $ U = {a,b}, V = {b,c} $ non sono disgiunti, hanno $ b $ in comune
• $ U = {a,b}, V = {b} $ non disgiunti
• $ U = {b}, V = {b,c} $ non disgiunti

Non esiste nessuna coppia di insiemi aperti non vuoti, disgiunti, la cui unione sia $ X $.

Pertanto, con la topologia $ A $ lo spazio topologico $ X $ è connesso.

2] Topologia B

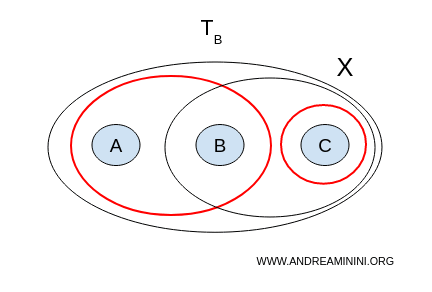
Cerco ora una separazione $ (U, V) $ con la topologia $ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $

• $ U = {a,b}, V = {b,c} $ non sono disgiunti, hanno $ b $ in comune
• $ U = {a,b}, V = {c} $ non vuoti, disgiunti e l'unione copre interamente lo spazio $ U \cup V = {a,b,c} = X $.

Quest'ultima coppia ( $ U = {a,b}, V = {c} $ ) soddisfa tutte le condizioni di separazione, quindi lo spazio $ X $ con la topologia B non è connesso.

Nota. Questo esempio mostra che la connessione dipende non solo dall’insieme sottostante, ma anche dalla scelta della topologia. Pur avendo lo stesso insieme di punti, le due topologie producono proprietà globali differenti: la prima mantiene la connessione, la seconda la rompe.

Esempio 2

Considero lo spazio $ X $ dove $ n $ è un numero reale fissato (ad esempio $ n = 0 $).

$$ X = (-\infty, n) \cup (n, +\infty) $$

Questo insieme è la retta reale privata di un punto, cioè:

$$ X = \mathbb{R} \setminus {n} $

Questo spazio è connesso o disconnesso?

Gli insiemi $ U = (-\infty, n) \quad \text{e} \quad V = (n, +\infty) $ sono entrambi:

• aperti nella topologia standard di $ \mathbb{R} $;
• disgiunti, perché non condividono alcun punto;
• non vuoti

L'unione degli insiemi $ U \cup V $ è proprio $ X $

$$ U \neq \emptyset, \quad V \neq \emptyset, \quad U \cap V = \emptyset, \quad U \cup V = X $$

Questa è esattamente la definizione di separazione dello spazio.

Pertanto lo spazio $ X = (-\infty, n) \cup (n, +\infty) $ è disconnesso, perché può essere diviso in due aperti disgiunti e non vuoti la cui unione restituisce tutto lo spazio.

Nota. In generale, togliendo un punto $ n $ dalla retta reale, ho “spezzato” la continuità. La retta si divide in due parti indipendenti, a sinistra e a destra di $ n $,  che non possono più essere collegate con un cammino continuo. Per questo motivo, lo spazio risulta anche non connesso per cammino oltre che disconnesso secondo la definizione topologia della separazione tramite insiemi aperti.

La differenza tra spazi connessi e spazi connessi per cammino

Gli spazi topologici connessi non coincidono sempre con gli spazi connessi per cammino.

Uno spazio topologico può essere connesso senza essere connesso per cammino (o per archi).

• Connessione topologica
  Lo spazio non può essere diviso in due insiemi aperti disgiunti e non vuoti la cui unione sia tutto lo spazio.
• Connessione per cammino
  Per ogni coppia di punti dello spazio esiste un cammino continuo che li collega interamente all’interno dello spazio. Se il cammino non passa due volte per uno stesso punto la connessione è detta connessione per archi.

In generale, ogni spazio connesso per cammino è anche connesso ma non vale il contrario.

Infatti, un cammino continuo tra due punti impedisce la possibilità di “tagliare” lo spazio in due regioni aperte separate.

Tuttavia, non vale il contrario perché esistono spazi connessi che non sono connessi per cammino.

Esempio. Un esempio classico è il vortice del topologo (topologist’s sine curve):$$ S = { (x, \sin(1/x)) \mid x > 0 } \cup { (0, y) \mid -1 \le y \le 1 } $$ Questo spazio è connesso, poiché non si può separare in due aperti disgiunti, ma non è connesso per cammino, perché non esiste un cammino continuo che colleghi un punto della parte oscillante con un punto della parte verticale

E così via.