Teorema di caratterizzazione degli spazi connessi tramite insiemi aperti e chiusi (clopen)

Uno spazio topologico \( X \) è connesso se e solo se gli unici sottoinsiemi aperti e chiusi (clopen) di \( X \) sono \( X \) e l'insieme vuoto \( \emptyset \).

In altre parole, uno spazio topologico è connesso se gli unici insiemi clopen sono i sottoinsiemi ibridi di \( X \).

Non esistono sottoinsiemi propri non vuoti, cioè diversi da \( X \) e da \( \emptyset \) che siano contemporaneamente aperti e chiusi (clopen).

Questo teorema fornisce una caratterizzazione molto utile della connessione topologica.

La spiegazione

In topologia, un insieme che è aperto e chiuso allo stesso tempo tende a separare lo spazio in due parti distinte.

Se ne esiste uno che non è banale, cioè diverso da \( X \) o \( \emptyset \), allora lo spazio si può dividere in due pezzi senza continuità fra loro.

Questo significa che lo spazio non è connesso.

Viceversa, se gli unici insiemi clopen sono l'insieme stesso \( X \) e l'insieme vuoto \( \emptyset \), ossia i sottoinsiemi ibridi, allora non c’è nessun modo di spezzare lo spazio in due parti separate. Quindi lo spazio è connesso.

Nota. In ogni spazio topologico, l'insieme stesso \( X \) e l'insieme vuoto \( \emptyset \) sono sempre aperti e chiusi.

Un esempio pratico

Considero l'insieme $ X=\{a,b,c,d \} $ con la topologia T che definisce "open" i seguenti sottoinsiemi: $ \{ b \}, \{ a,b \}, \{ c,d \}, \{ b,c,d \}, \{ a,b,c,d \}, \emptyset $.

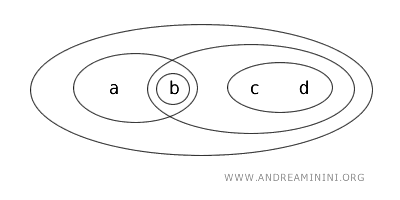
In questo caso l'insieme $ \{ a,b \} $ è un insieme clopen, sia aperto che chiuso.

• E' aperto perché è definito "open" dalla stessa topologia T
• E' chiuso perché il suo complemento $ X- \{a,b \} $ è un altro insieme aperto $ \{ c,d \} $

Da questo deduco che lo spazio topologico \( ( X, T ) \) non è connesso, perché esiste almeno un sottoinsieme proprio clopen.

Una sola occorrenza di un insieme di questo tipo è sufficiente per concludere che lo spazio non è connesso. Non serve cercarne altri.

La semplice presenza di un sottoinsieme clopen diverso da \( X \) e da \( \emptyset \) dimostra che lo spazio può essere suddiviso in due parti disgiunte e aperte $ \{ a,b \} $ e $ \{ c,d \} $, quindi mancano le condizioni necessarie per la connessione topologica dello spazio.

Esempio 2

Considero l’insieme dei numeri reali $ \mathbb{R} $ con la topologia normale, cioè quella definita dagli intervalli aperti (a, b).

In questo caso gli intervalli $ (a, b) $ sono **aperti, ma non chiusi, mentre gli intervalli  $[a, b] $ sono chiusi, ma non aperti.

Gli unici insiemi che sono aperti e chiusi insieme sono $ \mathbb{R} $ e \( \emptyset \).

Pertanto, l'insieme $ \mathbb{R} $  con la topologia standard è uno spazio topologico connesso.

Esempio 3

Considero lo spazio \( X = (0,1) \cup (2,3) \subset \mathbb{R} \) con la topologia indotta da $ \mathbb{R} $.

Gli insiemi $ (0,1) $ e $ (2,3) $ sono entrambi aperti in $ X $ e chiusi in $ X $, perché il loro complemento in $ X $ è l’altro intervallo aperto. Infatti:

• il complemento di $ (0,1) $ in $ X $ è $ (2,3) $, che è aperto in $ X $;
• il complemento di $ (2,3) $ in $ X $ è $ (0,1) $, anch’esso aperto in $ X $.

Quindi entrambi sono clopen.

Poiché esistono insiemi non banali che sono sia aperti che chiusi, posso affermare che lo spazio $ X $ non è connesso.

La disconnessione si manifesta proprio perché posso trovare due insiemi aperti (i due pezzi) che coprono tutto lo spazio senza toccarsi.

E così via.