Il prodotto diretto degli spazi vettoriali nella teoria delle categorie

Il prodotto diretto $V \times W$ di due spazi vettoriali $V$ e $W$ è definito come l'insieme di tutte le coppie ordinate $(v, w)$, dove $v \in V$ e $w \in W$. Ogni coppia può essere sommata o moltiplicata per uno scalare rispettando le seguenti regole:

Addizione
$(v, w) + (v', w') = (v+v', w+w')$
Moltiplicazione per uno scalare
$r(v, w) = (rv, rw)$

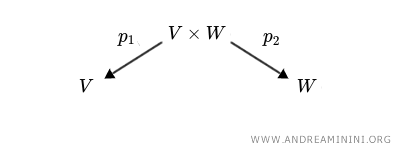
Introduco delle mappe di proiezione, ovvero delle funzioni che "proiettano" un elemento del prodotto diretto indietro nei suoi componenti originali:

$$ p_1(v, w) = v $$

$$ p_2(v, w) = w $$

Queste funzioni estraggono rispettivamente il primo e il secondo componente della coppia.

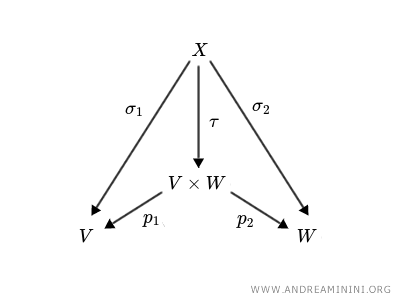
Per la proprietà universale dei prodotti diretti, se esistono trasformazioni $ \sigma_1: X \rightarrow V $ e $ \sigma_2: X \rightarrow W $, esiste una trasformazione unica

$$ \tau: X \rightarrow V \times W \text{ tale che } p_1 \circ \tau = \sigma_1 \ e \ p_2 \circ \tau = \sigma_2 $$

La trasformazione $ \tau $ combina essenzialmente le due trasformazioni $ \sigma_1 $ e $ \sigma_2 $ in una singola trasformazione che mantiene tutte le informazioni necessarie per recuperare $ \sigma_1 $ e $ \sigma_2 $ usando le mappe di proiezione.

Nota. Questa costruzione è importante perché mi permette di passare da lavorare separatamente in due spazi $V$ e $W$ a lavorare in un unico spazio $V \times W$, mantenendo la possibilità di recuperare facilmente i componenti originali grazie alle mappe di proiezione. È un modo per "unire" spazi vettoriali mantenendo l'accesso a ciascuno individualmente attraverso le proiezioni.

Un esempio pratico

Considero questi spazi vettoriali $ V $ e $ W $

$$ V = \mathbb{R}^2 $$

$$ W = \mathbb{R}^3 $$

Il prodotto diretto $ V \times W $ sarà l'insieme delle coppie $(v, w)$ dove:

$ v \in \mathbb{R}^2 $ ad esempio, vettori come $ (1,2) $
$ w \in \mathbb{R}^3 $ ad esempio, vettori come $ (3,4,5) $

Ad esempio, il vettore $ v $ potrebbe indicare la posizione (x,y) sul piano mentre il vettore $ w $ il colore del punto espresso con una terna di valori RGB ovvero (red, green, blue).

Una coppia tipica nel prodotto diretto $V \times W$ potrebbe essere $( (1,2), (3,4,5) )$.

Le operazioni sarebbero:

Addizione
Esempio $$ ( (1,2), (3,4,5) ) + ( (2,3), (1,1,1) ) $$ $$ ( (1+2, 2+3), (3+1, 4+1, 5+1) ) $$ $$ ( (3,5), (4,5,6) ) $$
Moltiplicazione per uno scalare
Esempio $$ 2 \cdot ( (1,2), (3,4,5) ) $$ $$ ( (2\cdot1, 2\cdot2), (2\cdot3, 2\cdot4, 2\cdot5) ) $$ $$ ( (2,4), (6,8,10) ) $$

Definisco delle mappe di proiezione

$p_1( (1,2), (3,4,5) ) = (1,2)$
$p_2( (1,2), (3,4,5) ) = (3,4,5)$

le mappe di proiezione

Secondo la proprietà universale, immagino di avere uno spazio vettoriale $ X $ su $ \mathbb{R} $ e due trasformazioni lineari

$$ \sigma_1 : X \to \mathbb{R}^2 $$

$$ \sigma_2 : X \to \mathbb{R}^3 $$

definite come:

$ \sigma_1(t) = (t, t^2) $
$ \sigma_2(t) = (t, 2t, 3t) $

Voglio trovare una trasformazione

$$ \tau : \ X \ \to \mathbb{R}^2 \times \mathbb{R}^3 \text{ tale che } p_1 \circ \tau = \sigma_1 \ e \ p_2 \circ \tau = \sigma_2 $$

Definisco

$$ \tau(t) = ( \sigma_1(t), \sigma_2(t) ) = ( (t, t^2), (t, 2t, 3t) ) $$

A questo punto verifico se $ p_1 \circ \tau = \sigma_1 $ e se $ p_2 \circ \tau = \sigma_2 $

$ p_1(\tau(t)) = p_1( (t, t^2), (t, 2t, 3t) ) = (t, t^2) $ che è $ \sigma_1(t) $
$ p_2(\tau(t)) = p_2( (t, t^2), (t, 2t, 3t) ) = (t, 2t, 3t) $ che è $ \sigma_2(t) $

Quindi $ \tau $ è la trasformazione lineare unica che combina le trasformazioni $ \sigma_1 $ e $ \sigma_2 $ nel prodotto diretto mantenendo la corrispondenza richiesta dalle mappe di proiezione.

la trasformazione lineare

Ad esempio se $ t = 1 $ vediamo cosa accade

$$ \sigma_1(1) = (1, 1^2) = (1, 1) $$

$$ \sigma_2(1) = (1, 2 \cdot 1, 3 \cdot 1) = (1, 2, 3) $$

Ora, se combino queste trasformazioni nella trasformazione $ \tau $, che è definita come:

$$ \tau(t) = (\sigma_1(t), \sigma_2(t)) $$

Sostituendo $ t = 1 $ ottengo:

$$ \tau(1) = (\sigma_1(1), \sigma_2(1)) = ((1, 1), (1, 2, 3)) $$

A questo punto verifico le mappe di proiezione:

$$ p_1(\tau(1)) = p_1((1, 1), (1, 2, 3)) = (1, 1) = \sigma_1(1) $$

$$ p_2(\tau(1)) = p_2((1, 1), (1, 2, 3)) = (1, 2, 3) = \sigma_2(1) $$

Questo esempio mostra come la trasformazione $ \tau $ effettivamente combina le informazioni di $ \sigma_1 $ e $ \sigma_2 $ e come le mappe di proiezione permettano di recuperare i componenti originali dai risultati di $ \tau $, confermando la correttezza delle operazioni nel prodotto diretto in base alla proprietà universale.

Spero che questo esempio numerico renda il concetto di prodotto diretto e mappe di proiezione più tangibile e facile da comprendere.

E così via