Serie assolutamente convergente
Una serie è detta assolutamente convergente se è convergente la serie dei valori assoluti della successione an. $$ \sum_{n=1}^{\infty} |a_n| = |a_1|+|a_2|+...+|a_n| = s $$
Tutte le serie assolutamente convergenti sono anche convergenti.
$$ \sum_{n=1}^{\infty } |a_n| = ass.conv. \ \Rightarrow \sum_{n=1}^{\infty } a_n = conv. $$
Non vale però il contrario. Non tutte le serie convergenti sono anche assolutamente convergenti.
A cosa serve la convergenza assoluta? Se una serie Σak soddisfa la convergenza assoluta Σ|ak|, allora soddisfa anche la convergenza semplice. Questa proprietà è alla base del criterio di convergenza assoluta. E' utile per studiare il carattere delle serie alternate e delle serie con termini anche negativi.
Un esempio pratico
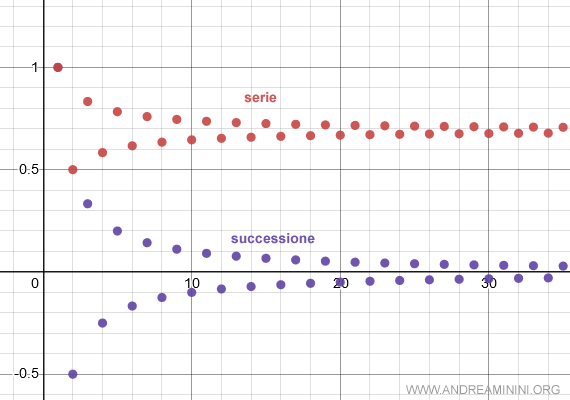
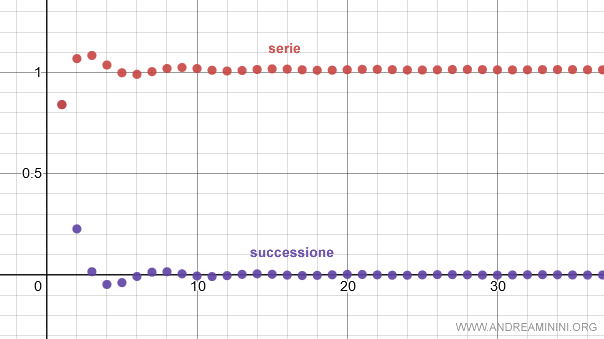
Questa serie alternata è una serie convergente
$$ \sum_{n=1}^{\infty} \frac{(-1)^n}{n^2} $$
Ecco la rappresentazione grafica
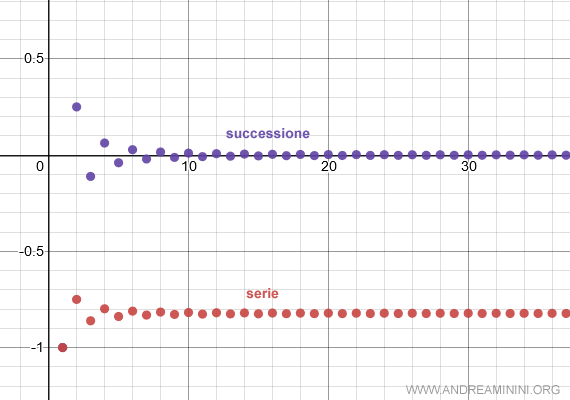
Per verificare se è anche una serie assolutamente convergente, studio il carattere della serie con i termini assoluti.
$$ \sum_{n=1}^{\infty} | \frac{(-1)^n}{n^2} | $$
Anche la serie con i termini assoluti è una serie convergente.
In questo caso, la serie è assolutamente convergente.
Esempio 2
La serie armonica alternata è una serie convergente.
$$ \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n} = l $$
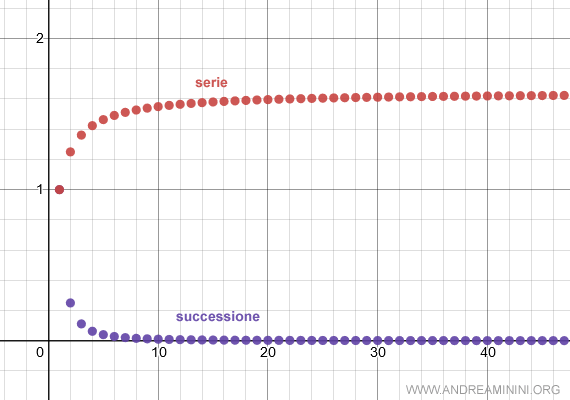
Ecco la rappresentazione grafica
Tuttavia, se considero il valore assoluto dei termini della successione an, la serie diventa una serie divergente.
$$ \sum_{n=1}^{\infty} | \frac{(-1)^{n-1}}{n} | = +\infty $$
Ecco la rappresentazione sul diagramma cartesiano.
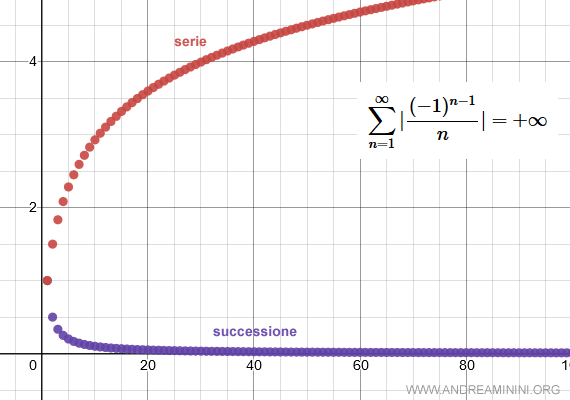
In questo caso, pur soddisfando la convergenza semplice, la serie non rispetta la convergenza assoluta.
Questo dimostra che una serie convergente potrebbe anche non essere assolutamente convergente.
II criterio della convergenza assoluta
Una serie assolutamente convergente è anche una serie convergente.
Non vale però il contrario. Una serie convergente (convergenza semplice) non è detto che sia anche una serie assolutamente convergente.
Questo criterio è utile per studiare il carattere delle serie alternate.
Esempio
Devo studiare la serie
$$ \sum_{n=1}^{\infty} \frac{\sin n}{n^2} $$
Non si tratta di una serie con termini non negativi, perché sin(n) può assumere valori da 1 a -1.
Per studiare il carattere della serie, verifico se la serie è assolutamente convergente.
$$ \sum_{n=1}^{\infty} | \frac{\sin n}{n^2} | $$
Questa serie è sicuramente inferiore di Σ 1/n2
$$ \sum_{n=1}^{\infty} | \frac{\sin n}{n^2} | \le \sum_{n=1}^{\infty} \frac{1}{n^2} $$
Studio il carattere della seconda serie per vedere se è convergente.
In questo caso, si tratta di una serie a termini positivi.
Pertanto, per studiare il carattere sella serie Σ 1/n2 posso usare uno dei criteri di convergenza delle serie non negative.
Opto per il criterio degli infinitesimi con p=2
$$ \lim_{n \rightarrow \infty} n^p \cdot a_n $$
$$ \lim_{n \rightarrow \infty} n^2 \cdot \frac{1}{n^2} = 1 $$
Poiché p>1 e il limite è diverso da infinito, per il criterio degli infinitesimi la serie Σ 1/n2 è convergente.
Se la serie Σ 1/n2 è convergente, per il criterio del confronto anche la prima serie Σ |sin n/n2| è convergente.
$$ \sum_{n=1}^{\infty} | \frac{\sin n}{n^2} | \le \sum_{n=1}^{\infty} \frac{1}{n^2} $$
O per meglio dire la serie Σ |sin n/n2| è assolutamente convergente.
Secondo il criterio di convergenza assoluta una serie assolutamente convergente è sempre convergente (convergenza semplice).
Pertanto, la serie iniziale Σ sin n/n2, quella senza il valore assoluto, è una serie convergente.
Ho così trovato il carattere della serie.
La dimostrazione del criterio di convergenza assoluta
Ho una serie con i termini al valore assoluto
$$ \sum_{k=1}^{\infty} |a_k| $$
Per ipotesi la serie è convergente.
Quindi, per il criterio di Cauchy esiste un valore ε che individua un indice v tale che per ogni n>v
$$ \sum_{k=n+1}^{\infty} |a_k| < ε $$
Nota. Dal punto di vista grafico.
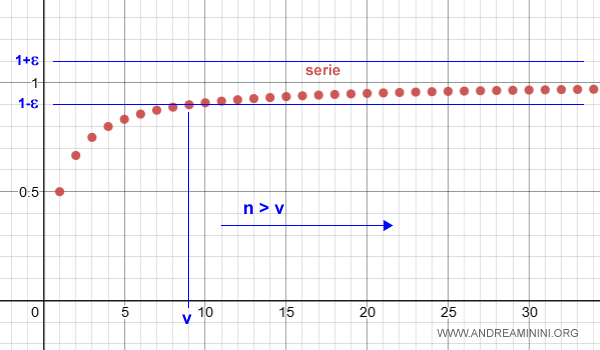
In generale, il criterio di Cauchy è soddisfatto per ogni serie ridotta da (n+1) a (n+p) dove p>0
$$ \sum_{k=n+1}^{n+p} |a_k| < ε $$
Considero la differenza tra il valore assoluto dei termini della serie e il valore assoluto della serie
$$ \sum_{k=n+1}^{n+p} |a_k| = |a_1|+|a_2|+|a_3|+... $$
$$| \sum_{k=n+1}^{n+p} a_k | = | a_1 + a_2 + a_3 + ... | $$
Secondo la proprietà della diseguaglianza triangolare
$$ | \sum_{k=n+1}^{n+p} a_k | \le \sum_{k=n+1}^{n+p} |a_k| $$
Poiché la seconda serie è inferiore di ε
$$ | \sum_{k=n+1}^{n+p} a_k | \le \sum_{k=n+1}^{n+p} |a_k| < ε $$
Secondo il teorema del confronto, se la seconda serie è convergente allora anche la prima serie è convergente.
Pertanto, anche la serie a termine generale è convergente per ogni n>v.
Dimostrazione alternativa
Per ipotesi questa serie è convergente
$$ \sum_{k=1}^{\infty} |a_k| $$
Quindi vale la seguente diseguaglianza
$$ \sum_{k=1}^{\infty} (|a_k| + a_k) \le \sum_{k=1}^{\infty} 2 \cdot |a_k| $$
perché il doppio del valore assoluto 2|ak| è sicuramente maggiore o uguale alla somma |ak|+ak.
La serie Σ |ak| è convergente per ipotesi. Pertanto, anche la serie Σ 2|ak| è convergente.
Ne consegue che, per il teorema del confronto, anche la serie Σ 2|ak|+ak è convergente.
Con qualche passaggio algebrico aggiuntivo
$$ \sum_{k=1}^{\infty} (|a_k| + a_k) \le \sum_{k=1}^{\infty} 2 \cdot |a_k| $$
$$ \sum_{k=1}^{\infty} |a_k| + \sum_{k=1}^{\infty} a_k \le \sum_{k=1}^{\infty} 2 \cdot |a_k| $$
$$ \sum_{k=1}^{\infty} a_k \le \sum_{k=1}^{\infty} 2 \cdot |a_k| - \sum_{k=1}^{\infty} |a_k| $$
$$ \sum_{k=1}^{\infty} a_k \le \sum_{k=1}^{\infty} |a_k| $$
Per il teorema del confronto delle serie anche la serie Σ ak è convergente.
Ho così dimostrato il teorema seguendo un procedimento alternativo.
E così via.
