Teorema degli infinitesimi sulle serie numeriche
Data una successione a termini non negativi an, preso un numero reale p qualsiasi, se esiste il limite della successione $$ l = \lim_{n \rightarrow \infty} n^p \cdot a_n $$ allora la serie an è convergente se $$ l \ne + \infty \:∧\: p>1 $$ o la serie an è divergente se $$ l \ne 0 \:∧\: p \le 1 $$
E' uno dei criteri di convergenza delle serie numeriche.
Un esempio pratico
Esempio 1
Ho la serie
$$ \sum_{n=1}^{ \infty } \frac{n+1}{2n^3-1} $$
Per studiare il carattere della serie, considero la successione
$$ a_n = \frac{n+1}{2n^3-1} $$
Poi studio il limite della successione per n elevato a p=2
$$ \lim_{n \rightarrow \infty} n^2 \cdot a_n $$
$$ \lim_{n \rightarrow \infty} n^2 \cdot \frac{n+1}{2n^3-1} $$
$$ \lim_{n \rightarrow \infty} \frac{n^3+n^2}{2n^3-1} = \frac{ \infty }{ \infty } $$
Il limite è una forma indeterminata del tipo ∞/∞
Per risolverlo uso il teorema di De L'Hopital
$$ \lim_{n \rightarrow \infty} \frac{3n^2+2n}{6n^2} = \frac{ \infty }{ \infty } $$
$$ \lim_{n \rightarrow \infty} \frac{6n+2}{12n} = \frac{ \infty }{ \infty } $$
$$ \lim_{n \rightarrow \infty} \frac{6}{12} = \frac{1}{2} $$
Il limite esiste ed è diverso da infinito.
Pertanto, essendo p>1 e l≠∞, secondo il teorema degli infinitesimi la serie è una serie convergente
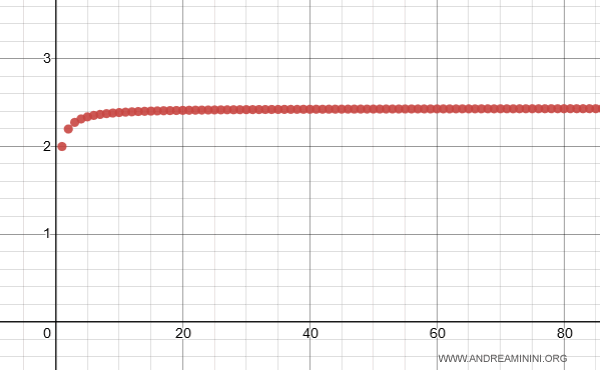
$$ \sum_{n=1}^{ \infty } \frac{n+1}{2n^3-1} $$
Ecco la rappresentazione grafica.
Esempio 2
Ho la serie
$$ \sum_{n=1}^{ \infty } \frac{n-1}{n+1} $$
Considero la successione
$$ a_n = \frac{n+1}{n-1} $$
Calcolo il limite della successione per n elevato a p=2
$$ \lim_{n \rightarrow \infty} n^2 \cdot a_n $$
$$ \lim_{n \rightarrow \infty} n^2 \cdot \frac{n-1}{n+1} $$
$$ \lim_{n \rightarrow \infty} \frac{n^3-n^2}{n+1} = \frac{ \infty }{ \infty } $$
E' una forma indeterminata che mi permette di usare il teorema di De L'Hopital per calcolare il limite
$$ \lim_{n \rightarrow \infty} \frac{3n^2-2n}{1} = \infty $$
Il limite tende a infinito ma, essendo p>1, non posso affermare che sia convergente.
Quindi, provo a moltiplicare la successione per p=1 per capire se è divergente.
$$ \lim_{n \rightarrow \infty} n \cdot a_n $$
$$ \lim_{n \rightarrow \infty} n \cdot \frac{n-1}{n+1} $$
$$ \lim_{n \rightarrow \infty} \frac{n^2-n}{n+1} = \frac{ \infty }{ \infty } $$
Poi applico il teorema di De L'Hopital
$$ \lim_{n \rightarrow \infty} \frac{2n-1}{1} = + \infty $$
Il limite è infinito e p≤1.
Pertanto, secondo il teorema degli infinitesimi la serie è una serie divergente.
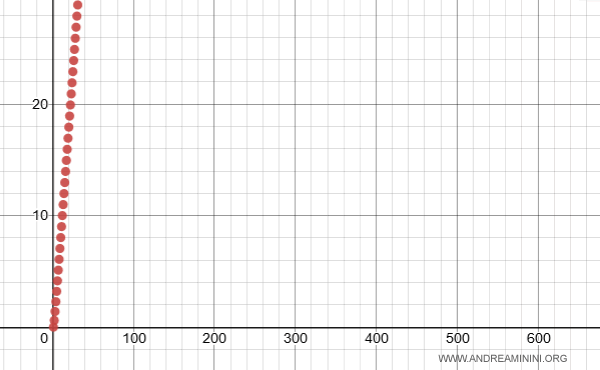
$$ \sum_{n=1}^{ \infty } \frac{n-1}{n+1} = + \infty $$
Ecco la rappresentazione grafica della serie
La dimostrazione
A] Serie convergente
Secondo il teorema degli infinitesimi una serie è convergente se esiste un limite finito con p>1
$$ l = \lim_{n \rightarrow \infty} n^p \cdot a_n $$
Se esiste un limite finito, allora per qualsiasi ε>0 esiste un indice v tale che per ogni n>v si ha
$$ n^p \cdot a_n < l + ε $$
Per ipotesi ε=1.
$$ n^p \cdot a_n < l + 1 $$
Pertanto, per ogni n>v vale la diseguaglianza
$$ 0 \le n^p \cdot a_n < l+1 \:\:\:\: \forall n>v $$
che equivale a
$$ 0 \le a_n < \frac{l+1}{n^p} $$
Applico la sommatoria a tutti i membri della disequazione
$$ 0 \le \sum_{n=1}^{\infty} a_n < \sum_{n=1}^{\infty} \frac{l+1}{n^p} $$
L'ultimo termine della disequazione è una serie armonica generalizzata che per p>1 è una serie convergente.
Per il teorema del confronto anche la serie an è convergente.
A] Serie divergente
Secondo il teorema degli infinitesimi una serie è divergente se esiste un limite diverso da zero con p≤1
$$ l = \lim_{n \rightarrow \infty} n^p \cdot a_n \ne 0 $$
Quindi, esiste un indice v tale che per ogni n>v vale la seguente diseguaglianza
$$ n^p \cdot a_n > \frac{l}{2} $$
con un semplice passaggio algebrico
$$ a_n > \frac{l}{2 \dot n^p} $$
$$ a_n > \frac{l}{2} \cdot \frac{1}{n^p} $$
Applico la sommatoria a entrambi i membri
$$ \sum_{n=1}^{\infty} a_n > \sum_{n=1}^{\infty} \frac{l}{2} \cdot \frac{1}{n^p} $$
La serie al secondo membro contiene la serie armonica generalizzata che per p≤1 è una serie divergente.
$$ \sum_{n=1}^{\infty} a_n > \infty $$
Pertanto, secondo la diseguaglianza anche la serie an deve essere divergente.
E così via.
