La serie armonica generalizzata

La serie armonica generalizzata è la seguente: $$ \sum_{k=1}^{\infty} \frac{1}{(k)^p} $$ dove p è un numero reale positivo qualsiasi.

La serie armonica generalizzata è particolare perché modifica il carattere a seconda del valore del parametro p.

• Per p≤1 la serie è divergente
• Per p>1 la serie è convergente

Un esempio pratico

Ecco la serie armonica generalizzata per p=1.

E' la serie armonica classica e pertanto è divergente.

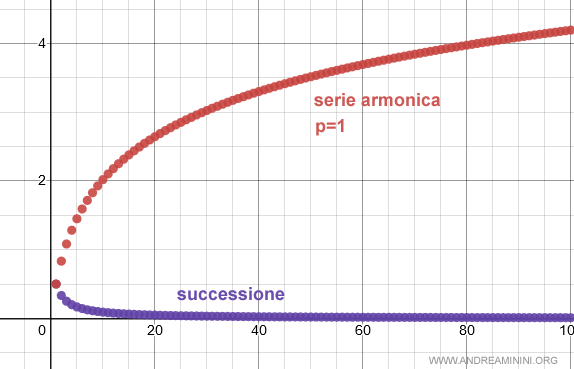
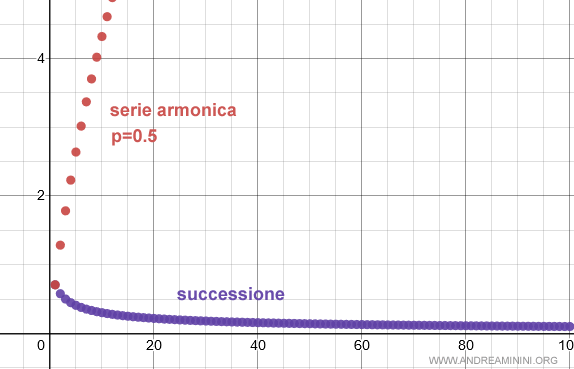
Per 0<p<1 la serie armonica è sempre divergente.

Ad esempio, per p=0.5 il grafico della serie è

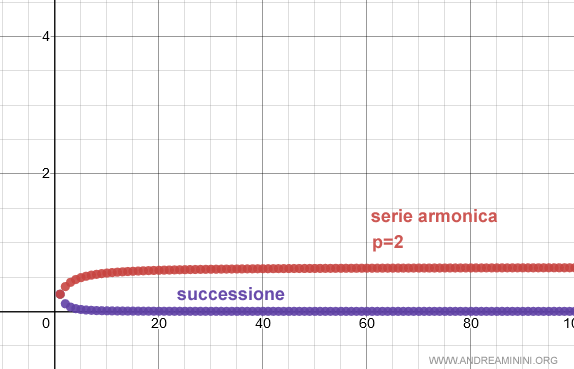
Per p>1, invece, la serie armonica cambia carattere perché diventa convergente.

Ad esempio, per p=2 il grafico della funzione è

La dimostrazione

Considero tre casi distinti:

• p=1
• p>1
• p<1

Il caso p=1 (serie armonica semplice)

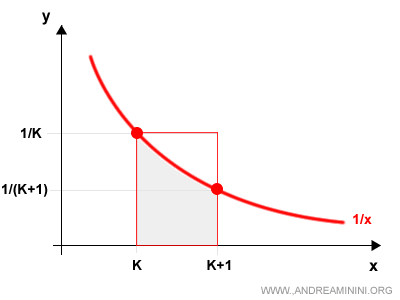
Prendo in considerazione un intervallo [k, k+1].

Per ogni valore x compreso nell'intervallo [k, k+1] vale.

$$ k \le x \le k+1 $$

Nella serie armonica generalizzata valgono le seguenti diseguaglianze.

$$ \frac{1}{(k+1)^p} \le \frac{1}{x^p} \le \frac{1}{k^p} \:\:\: \forall x \in [k,k+1] $$

Quindi, per ogni x>k vale

$$ \frac{1}{x^p} \le \frac{1}{k^p} $$

Calcolo l'integrale nell'intervallo [k,k+1] di entrambi i termini della disequazione

$$ \int_k^{k+1} \frac{1}{x^p} \:dx \le \int_k^{k+1} \frac{1}{k^p} \:dx $$

Poiché 1/k è una costante, posso spostarla fuori dall'integrale

$$ \int_k^{k+1} \frac{1}{x^p} \:dx \le \frac{1}{k^p} \int_k^{k+1} \:dx $$

L'integrale nel membro di destra è uguale a 1.

$$ \int_k^{k+1} \frac{1}{x^p} \:dx \le \frac{1}{k^p} $$

La precedente disequazione confronta l'area al di sotto della funzione 1/x nell'intervallo [k,k+1] con l'area rettangolare 1/k·(k+1-k) = 1/k

In entrambi i membri della disequazione applico la sommatoria per k da 1 a n

$$ \sum_{k=1}^n \int_k^{k+1} \frac{1}{x^p} \:dx \le \sum_{k=1}^n \frac{1}{k^p} $$

Poiché p=1.

$$ \sum_{k=1}^n \int_k^{k+1} \frac{1}{x} \:dx \le \sum_{k=1}^n \frac{1}{k} $$

Riscrivo la sommatoria dell'integrale al primo membro in questa forma equivalente

$$ \int_1^{n+1} \frac{1}{x} \:dx \le \sum_{k=1}^n \frac{1}{k} $$

Poi risolvo l'integrale

$$ \log (n+1) - \log(1) \le \sum_{k=1}^n \frac{1}{k} $$

poiché il logaritmo di 1 è zero

$$ \log (n+1) - 0 \le \sum_{k=1}^n \frac{1}{k} $$

$$ \log (n+1) \le \sum_{k=1}^n \frac{1}{k} $$

Il secondo membro della disequazione è una ridotta n-sima della serie armonica.

Calcolo il limite per n che tende a infinito in entrambi i membri.

$$ \lim_{n \rightarrow \infty} \log (n+1) \le \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{1}{k} $$

Il limite del logaritmo è infinito

$$ \infty \le \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{1}{k} $$

Pertanto, il limite della serie armonica è sicuramente infinito.

La serie armonica con p=1 è divergente.

Il caso p>1 (serie convergente)

Prendo in considerazione un intervallo [k, k+1].

Per ogni valore x compreso nell'intervallo [k, k+1] vale.

$$ k \le x \le k+1 $$

Nella serie armonica generalizzata valgono le seguenti diseguaglianze.

$$ \frac{1}{(k+1)^p} \le \frac{1}{x^p} \le \frac{1}{k^p} \:\:\: \forall x \in [k,k+1] $$

Calcolo l'integrale da k a k+1 in tutti i membri della diseguaglianza

$$ \int_k^{k+1} \frac{1}{(k+1)^p} \: dx \le \int_k^{k+1} \frac{1}{x^p} \: dx \le \int_k^{k+1} \frac{1}{k^p} \: dx $$

$$ \frac{1}{(k+1)^p} \int_k^{k+1} \: dx \le \int_k^{k+1} \frac{1}{x^p} \: dx \le \frac{1}{k^p} \int_k^{k+1} \: dx $$

Risolvo il primo e il terzo integrale con la formula fondamentale dell'integrazione.

$$ \frac{1}{(k+1)^p} \cdot [(k+1)-k] \le \int_k^{k+1} \frac{1}{x^p} \: dx \le \frac{1}{k^p} \cdot [(k+1)-k] $$

$$ \frac{1}{(k+1)^p} \le \int_k^{k+1} \frac{1}{x^p} \: dx \le \frac{1}{k^p} $$

Poi applico la sommatoria da k=1 a n a tutti i membri della diseguaglianza.

$$ \sum_{k=1}^n \frac{1}{(k+1)^p} \le \sum_{k=1}^n \int_k^{k+1} \frac{1}{x^p} \: dx \le \sum_{k=1}^n \frac{1}{k^p} $$

Applico la proprietà additiva degli integrali definiti e riscrivo l'elemento intermedio in una forma equivalente più compatta

$$ \sum_{k=1}^n \frac{1}{(k+1)^p} \le \int_1^{n+1} \frac{1}{x^p} \: dx \le \sum_{k=1}^n \frac{1}{k^p} $$

Spiegazione. Sviluppando la serie del primo membro. $$ \sum_{k=1}^n \int_{k}^{k+1} \frac{1}{x^p} \: dx = \int_{1}^{2} \frac{1}{x^p} \: dx + \int_{2}^{3} \frac{1}{x^p} \: dx + \int_{3}^{4} \frac{1}{x^p} \: dx + ... + \int_{n}^{n+1} \frac{1}{x^p} \: dx $$ E' evidente che si tratta della somma della superficie sotto il grafico della funzione 1/x^p da 1 a n+1. Pertanto, posso scrivere in modo equivalente. $$ \sum_{k=1}^n \int_{k}^{k+1} \frac{1}{x^p} \: dx = \int_{1}^{n+1} \frac{1}{x^p} \: dx $$

Sapendo che la serie armonica n-esima è

$$ s_n = \sum_{k=1}^{n} \frac{1}{k} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + ... + \frac{1}{n} $$

La sommatoria al primo membro è la serie armonica s_n senza il primo termine iniziale (1) e con l'aggiunta di un termine 1/n+1 alla fine.

$$ \sum_{k=1}^{n} \frac{1}{k+1} = \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + ... + \frac{1}{n+1} $$

Quindi posso considerarla come ridotta n+1-esima della serie armonica meno 1

$$ \sum_{k=1}^{n} \frac{1}{k+1} = s_{n+1} - 1 $$

Sostituisco il primo membro nella disequazione

$$ s_{n+1} -1 \le \int_1^{n+1} \frac{1}{x^p} \: dx \le \sum_{k=1}^n \frac{1}{k^p} $$

La sommatoria all'ultimo membro della disequazione è uguale alla ridotta n-esima della serie armonica

$$ \sum_{k=1}^{n} \frac{1}{k} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + ... + \frac{1}{n} = s_n $$

Quindi posso considerarla come ridotta n-esima della serie armonica.

Sostituisco l'ultimo membro nella disequazione

$$ s_{n+1} -1 \le \int_1^{n+1} \frac{1}{x^p} \: dx \le s_n $$

Calcolo l'integrale nel membro intermedio della disequazione

$$ s_{n+1} -1 \le \begin{bmatrix} \frac{x^{1-p}}{1-p} \end{bmatrix} _1^{n+1} \le s_n $$

$$ s_{n+1} -1 \le \frac{(n+1)^{1-p}}{1-p} - \frac{1^{1-p}}{1-p} \le s_n $$

$$ s_{n+1} -1 \le \frac{(n+1)^{1-p}}{1-p} - \frac{1}{1-p} \le s_n $$

Sposto il -1 dal membro di sinistra all'elemento intermedio della disequazione

$$ s_{n+1} \le 1 + \frac{(n+1)^{1-p}}{1-p} - \frac{1}{1-p} \le s_n $$

Poi calcolo il limite per n che tende a infinito

$$ \lim_{n \rightarrow \infty} s_{n+1} \le \lim_{n \rightarrow \infty} 1 + \frac{(n+1)^{1-p}}{1-p} - \frac{1}{1-p} \le \lim_{n \rightarrow \infty} s_n $$

Non considero l'ultimo termine della diseguaglianza.

Quindi, riscrivo la diseguaglianza usando i primi due componenti.

$$ \lim_{n \rightarrow \infty} s_{n+1} \le \lim_{n \rightarrow \infty} 1 + \frac{(n+1)^{1-p}}{1-p} - \frac{1}{1-p} $$

Il secondo limite è un limite convergente

Spiegazione. Studio il limite dell'elemento centrale. $$ \lim_{n \rightarrow \infty} 1 + \frac{(n+1)^{1-p}}{1-p} - \frac{1}{1-p} $$ I termini 1 e 1/(1-p) sono costanti rispetto a n. Pertanto, il limite dipende dal solo termine (n+1)^1-p/(1-p) $$ 1 - \frac{1}{1-p} + \lim_{n \rightarrow \infty} \frac{(n+1)^{1-p}}{1-p} $$ Poiché per p>1 il termine 1-p è negativo, la successione tende a zero per n→∞ $$ \lim_{n \rightarrow \infty} \frac{(n+1)^{1-p}}{1-p} = 0 $$ Quindi $$ 1 - \frac{1}{1-p} + 0 $$ ossia $$ \lim_{n \rightarrow \infty} 1 + \frac{(n+1)^{1-p}}{1-p} - \frac{1}{1-p} = 1 - \frac{1}{1-p} $$ Pertanto il limite intermedio è convergente.

Se il limite intermedio è convergente per p>1, allora per il teorema del confronto delle serie anche la serie s_n+1 è convergente. Non può essere divergente.

$$ \lim_{n \rightarrow \infty} s_{n+1} \le 1 - \frac{1}{1-p} $$

Quindi, la serie armonica generalizzata per p>1 è convergente.

$$ \lim_{n \rightarrow \infty} \sum_{k=1}^{n+1} \frac{1}{k^p} = \: convergente \:\:\: per \:\: p>1 $$

Il caso p<1 (serie divergente)

Riprendo la dimostrazione del caso p>1 fino a

$$ s_{n+1} -1 \le \frac{(n+1)^{1-p}}{1-p} - \frac{1}{1-p} \le s_n $$

e calcolo il limite per n che tende a infinito

$$ \lim_{n \rightarrow \infty} s_{n+1} -1 \le \lim_{n \rightarrow \infty} \frac{(n+1)^{1-p}}{1-p} - \frac{1}{1-p} \le \lim_{n \rightarrow \infty} s_n $$

Non considero il primo termine della diseguaglianza.

Quindi, riscrivo la diseguaglianza usando gli ultii due componenti.

$$ \lim_{n \rightarrow \infty} \frac{(n+1)^{1-p}}{1-p} - \frac{1}{1-p} \le \lim_{n \rightarrow \infty} s_n $$

In questo caso per p<1 il limite a sinistra diverge a infinito

Spiegazione. Studio il limite dell'elemento centrale. $$ \lim_{n \rightarrow \infty} \frac{(n+1)^{1-p}}{1-p} - \frac{1}{1-p} $$ Il termine 1/(1-p) è costante rispetto a n. Pertanto, il limite dipende dal solo termine (n+1)^1-p/(1-p) $$ \lim_{n \rightarrow \infty} \frac{(n+1)^{1-p}}{1-p} $$ Poiché per p<1 il termine 1-p è sempre positivo. Pertanto, la successione tende a infinito per n→∞ $$ \lim_{n \rightarrow \infty} \frac{(n+1)^{1-p}}{1-p} = \infty $$

Se il limite a sinistra è divergente, allora per il teorema del confronto anche la serie s_n è divergente.

$$ \infty \le \lim_{n \rightarrow \infty} s_n $$

Quindi, la serie armonica generalizzata per p<1 è divergente.

$$ \lim_{n \rightarrow \infty} \sum_{k=1}^{n} \frac{1}{k^p} = \: \infty \:\:\: per \:\: p<1 $$

Il caso p≤0 (serie divergente)

Se p≤0 la serie è sicuramente divergente perché il suo termine n-esimo non tende a zero.

Quindi, la condizione necessaria di convergenza della serie non è soddisfatta.

$$ \lim_{k \rightarrow \infty} \frac{1}{k^p} = \infty \ne 0 \:\:\:\:\: con \:\: p \le 0 $$

Essendo una serie a termini non negativi, la serie non può essere indeterminata.

Pertanto, per esclusione la serie è divergente con p≤0.

$$ \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{1}{k^p} = \infty \:\:\:\:\: con \:\: p \le 0 $$

E così via.