Serie a termini non negativi
Una serie è a termini non negativi se per ogni n di N la serie è maggiore o uguale a zero. $$ a_n = \sum_{k=1}^{n} a_k \ge 0 \:\:\:\:\:\: \forall k \in N $$
Se i termini della serie sono tutti maggiori di zero, la serie è detta serie a termini positivi.
Un esempio pratico
Questa serie è a termini non negativi
$$ \sum_{k=1}^{\infty} \frac{1}{a_k} $$
perché ogni termine della serie ha un valore non negativo
$$ a_1 = 1 \\ a_2 = 1 + \frac{1}{2} \\ a_3 = 1 + \frac{1}{2} + \frac{1}{3} \\ a_4 = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} \\ \vdots $$
Ecco la rappresentazione della serie sul diagramma cartesiano
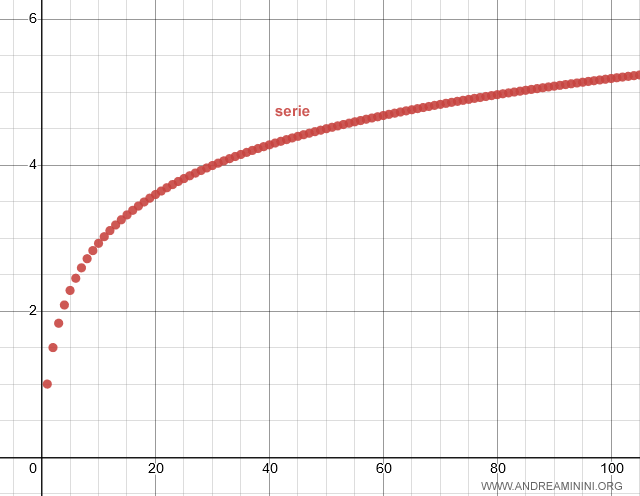
Teorema delle serie a termini non negativi
Una serie a termini non negativi è convergente o divergente. Non può essere indeterminata
Dimostrazione
Essendo sempre positiva (an≥0) la successione delle somme parziali della serie è una successione monotòna crescente.
$$ s_{n+1} = s_n + a_{n+1} \ge s_n $$
Poiché è crescente, secondo il teorema delle successioni monotòne, una successione monotòna ammette sempre un limite finito o infinito.
Pertanto, la serie può essere convergente o divergente ma non può essere indeterminata.
Un esempio pratico
Esempio 1
Questa serie è a termini non negativi
$$ \sum_{k=1}^{\infty} \frac{1}{k} $$
Pertanto, ammette sicuramente un limite delle somme parziali per n che tende a infinito.
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^{n} \frac{1}{k} $$
Per verificare se è convergente o divergente, calcolo il limite dei termini an
$$ \lim_{n \rightarrow \infty} \frac{1}{k} = 0 $$
Il fatto che la successione delle somme parziali sia infinitesima è una condizione necessaria ma non sufficiente per la convergenza della serie.
Per verificare la convergenza occorre usare un altro metodo.
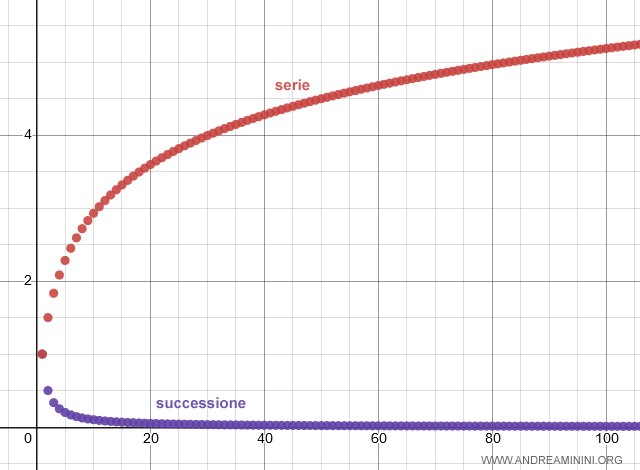
Nota. In questo caso la serie è divergente (serie armonica).
Esempio 2
Quest'altra serie è a termini non negativi
$$ \sum_{k=1}^{\infty} \frac{k}{k+1} $$
Quindi ammette un limite finito o infinito.
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^{n} \frac{k}{k+1} $$
Per verificare se la serie è convergente o divergente, calcolo il limite della successione dei termini.
$$ \lim_{n \rightarrow \infty} \frac{k}{k+1} = 1 $$
In questo caso il limite della successione dei termini non tende a zero.
Pertanto, se la serie non è convergente (e non è indeterminata) allora è sicuramente una serie divergente.
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^{n} \frac{k}{k+1} = +\infty $$
Ecco la rappresentazione grafica
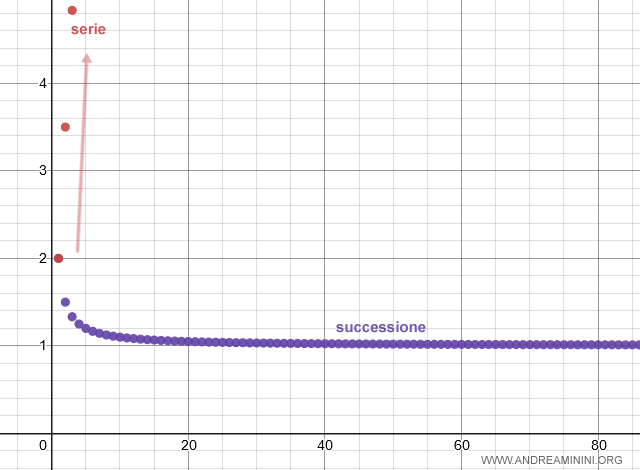
E così via.
