Il punto medio di un segmento
Il punto medio di un segmento AB è un punto che si trova alla stessa distanza dagli estremi A e B.
Per ogni segmento di lunghezza non nulla, esiste uno e un solo punto medio che lo divide in due segmenti congruenti.
Ad esempio, ho il segmento AB
Il segmento è composto da infiniti punti. Tuttavia, un solo punto riesce a dividerlo in due segmenti congruenti, ossia di pari lunghezza.
In questo caso il punto medio è il punto C.
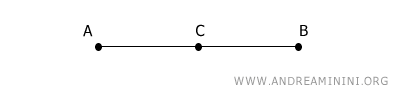
Il punto C divide il segmento AB in due segmenti AC e BC.
I due segmenti AC e BC sono congruenti tra loro.
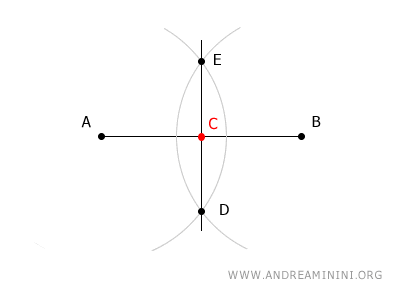
Come trovare il punto medio del segmento? Per individuare il punto medio di un segmento è sufficiente utilizzare un compasso e tracciare due archi con centro gli estremi del segmento e apertura a piacere purché maggiore della metà del segmento. Le intersezioni dei due archi determinano due punti D e E della retta che interseca il segmento AB nel suo punto medio C.
Dati due punti del piano $ A(x_A;y_A) $ e $ B(x_B;y_B) $ che individuano gli estremi di un segmento AB, il punto medio M del segmento ha le seguenti coordinate:
$$ x_M = \frac{x_A+x_B}{2} $$
$$ y_M = \frac{y_A+y_B}{2} $$
Le coordinate del punto medio M sono le semisomme delle ascisse e delle ordinate.E così via.
Come si calcola il punto medio
Le coordinate M(xM;yM) del punto medio M di un segmento sul piano cartesiano sono composte dalla semisomma delle ascisse e delle ordinate agli estremi A(xA;yA) e B(xB;yB) del segmento.
L'ascissa del punto medio è la media aritmetica delle ascisse agli estremi xA e xB del segmento
$$ x_M = \frac{x_A+x_B}{2} $$
L'ordinata del punto medio è la media aritmetica delle ordinate agli estremi yA e yB del segmento
$$ y_M = \frac{y_A+y_B}{2} $$
Un esempio pratico
Considero un segmento AB con estremi A(2;3) e B(6;5)
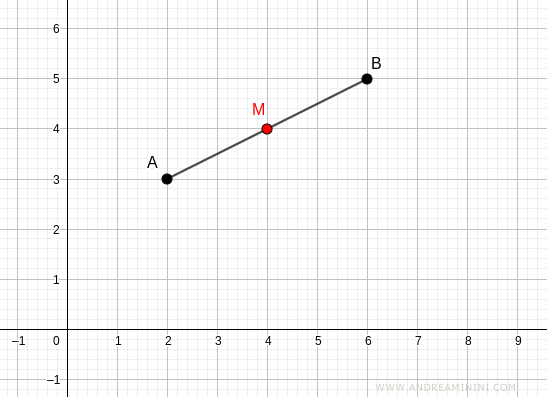
Le coordinate del punto medio sono
$$ x_M = \frac{2+6}{2} = 4 $$
$$ y_M = \frac{3+5}{2} = 4 $$
Il punto medio M del segmento AB si trova alle coordinate (4;4)
Esempio 2
Il segmento AB ha gli estremi nei punti A(2;1) e B(6;3).
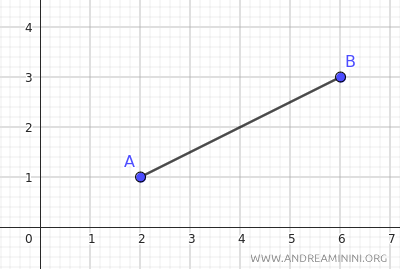
Il punto A si trova alle coordinate (2;1) ovvero xA=2 e yA=1 mentre il punto B si trova alle coordinate (6;3) ovvero xB=6 e yB=3.
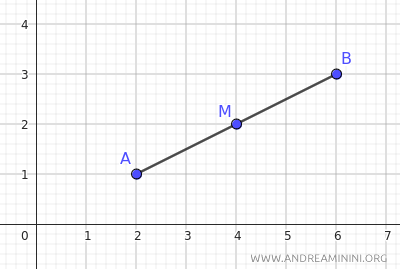
Calcolo le coordinate del punto medio M del segmento AB.
$$ x_M = \frac{x_A+x_B}{2} = \frac{2+6}{2} = \frac{8}{2} = 4 $$
$$ y_M = \frac{y_A+y_B}{2} = \frac{1+3}{2} = \frac{4}{2} = 2 $$
Il punto medio del segmento si trova alle coordinate (xM;yM)=(4;2).
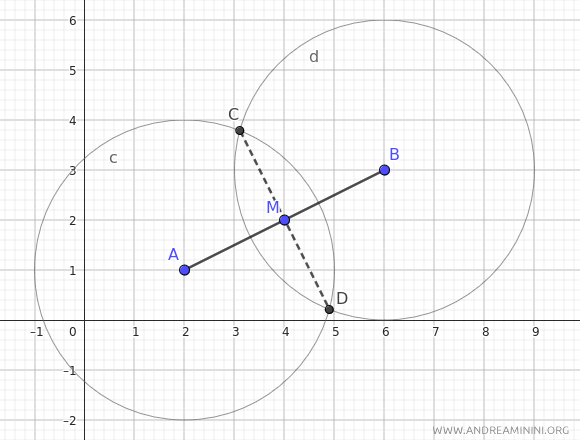
Per verificarlo basta disegnare due archi o due cerchi con lo stesso raggio, purché il raggio sia superiore alla lunghezza di AM, centrati su A e su B. Poi tracciare un segmento che ha per estremi i punti di intersezione C e D degli archi. Il segmento CD interseca il segmento AB nel punto medio M.
La dimostrazione
Considero il segmento AB e il punto medio M.
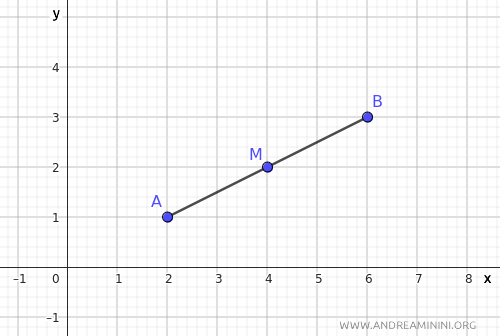
Traccio le rette parallele all'asse y passanti per i punti A, M, B.
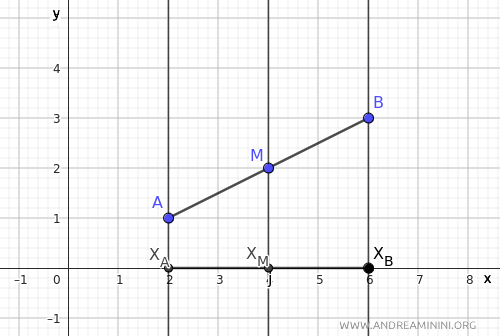
Le tre rette parallele sono tagliate da due trasversali AB e xAxB.
Per il teorema del fascio improprio di rette parallele allora i segmenti a segmenti congruenti su una trasversale corrispondono segmenti congruenti sull'altra trasversale.
Per ipotesi iniziale M è il punto medio di AB, quindi i segmenti AM≅BM sono congruenti. Questo implica che anche i segmenti corrispondenti xAxM≅xMxB sono congruenti.
In altre parole, se il punto M dimezza il segmento AB, allora dimezza anche il segmento XAXB.
$$ | x_M - x_A | = | x_B - x_M | $$
Poiché xA<xM<xB posso eliminare il valore assoluto.
$$ x_M - x_A = x_B - x_M $$
Ricavo xM
$$ x_M + x_M = x_B + x_A $$
$$ 2x_M = x_B + x_A $$
$$ x_M = \frac{ x_B + x_A }{2} $$
Ho trovato la proiezione sull'asse x del punto medio del segmento AB.
A questo punto ripeto la stessa procedura per calcolare la proiezione del punto medio M sull'asse y.
Traccio tre rette parallele all'asse x passanti per i punti A, B, M.
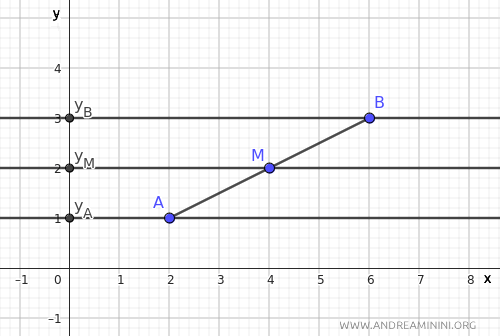
Anche in questo caso le tre rette parallele sono tagliate da due trasversali AB e yAyB.
Per il teorema del fascio improprio di rette parallele allora i segmenti se i segmenti AM≅BM sono congruenti, allora sono congruenti anche i segmenti corrispondenti yAyM≅yMyB.
In altre parole se M divide a metà il segmento AB, allora divide a metà anche la sua proiezione yAyB sull'asse y.
$$ | y_M - y_A | = | y_B - y_M | $$
Poiché yA<yM<yB posso eliminare il valore assoluto.
$$ y_M - y_A = y_B - y_M $$
Ricavo yM
$$ y_M + y_M = y_B + y_A $$
$$ 2y_M = y_B + y_A $$
$$ y_M = \frac{ y_B + y_A }{2} $$
Ho trovato la proiezione del punto medio del segmento AB sull'asse delle ordinate y.
Riepilogando, le coordinate del punto medio M del segmento AB sono:
$$ x_M = \frac{ x_B + x_A }{2} $$
$$ y_M = \frac{ y_B + y_A }{2} $$
E così via.
