Velocità istantanea
Cos'è la velocità istantanea
La velocità istantanea misura la velocità dello spostamento di un corpo in un singolo istante/posizione.
Come la velocità media anche per la velocità istantanea è opportuno distinguere tra lo spazio unidirezionale (retta) e multidirezionale (spazio a due o più dimensioni).
La velocità istantanea sulla retta
Quando un corpo si muove in una retta la direzione è nota. Può soltanto variare il verso.
In questo caso la velocità è una grandezza scalare ossia un numero.
Come si calcola la velocità media?
Per calcolare la velocità istantanea, analizzo dalla velocità media di un punto in un intervallo di tempo Δt=t2-t1.
$$ Δt = t_2 - t_1 $$
Utilizzo la legge oraria del moto per calcolare la posizione del corpo nell'istante iniziale x(t1) e finale x(t2).
La differenza tra le due posizione misura lo spazio percorso Δx dal corpo sulla retta.
$$ Δx = x(t_2) - x_(t_1) $$
Posso rappresentare lo spostamento su un diagramma cartesiano ponendo lo spazio x sulle ordinate e il tempo t sulle ascisse.
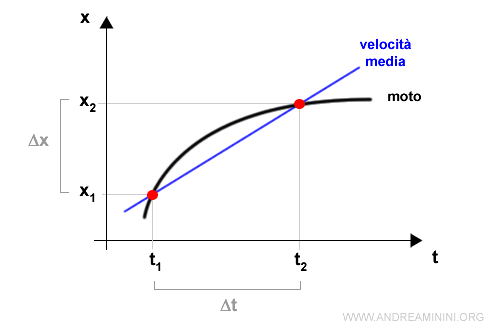
La differenza tra lo spazio percorso Δx e l'intervallo di tempo Δt mi fornisce la velocità media del punto.
$$ v = \frac{Δx}{Δt} = \frac{x_2-x_1}{Δt} $$
Dal punto di vista geometrico, nel diagramma precedente la velocità media è il coefficiente angolare della retta secante (blu) tra il punto iniziale e finale.
Nota. Essendo un rapporto tra due numeri scalari anche la velocità media sulla retta è una grandezza scalare.
Per calcolare la velocità istantanea del corpo nel punto iniziale x1 devo ridurre l'intervallo di tempo Δt fino a livelli infinitesimali.
$$ \lim_{ Δt \rightarrow 0} \frac{Δx}{Δt} $$
Man mano che l'intervallo si riduce, la retta secante indica la velocità media in un intervallo di tempo sempre più piccolo.
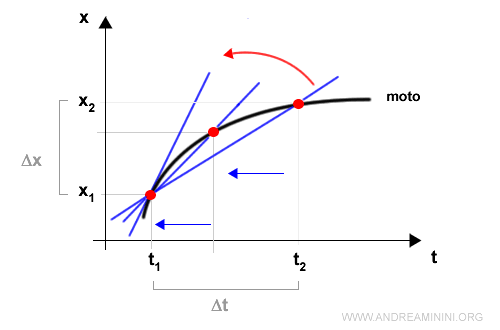
Quando l'intervallo di tempo Δt è infinitesimale la retta diventa una tangente del punto/istante iniziale.
Il coefficiente della retta tangente è la velocità istantantanea nell'istante t1.
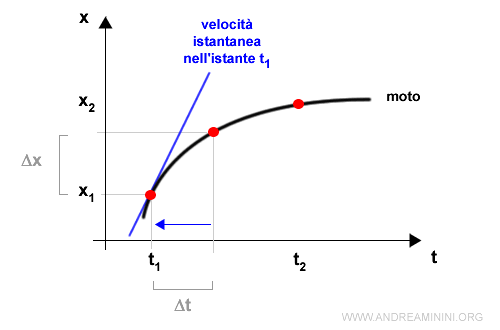
Scegliendo un punto iniziale diverso, posso usare lo stesso procedimento per calcolare la velocità istantanea in ogni istante t .
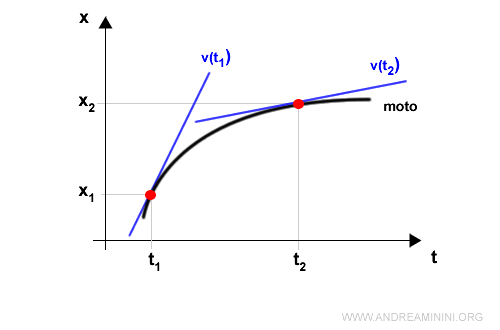
L'inclinazione della retta tangente indica la velocità del punto in ogni istante.
Quando la retta tangente è completamente orizzontale, il corpo è fermo.
Esempio. Nell'istante t1 la retta tangente è più inclinata rispetto a quella dell'istante t2. Questo vuol dire che la velocità è maggiore nell'istante iniziale rispetto a quello finale. Nel corso del tempo il corpo ha rallentato il suo moto.
La velocità istantanea sul piano
Nel caso della velocità istantanea sul piano, o in uno spazio a più dimensioni, la velocità è una grandezza vettoriale, perché il punto può muoversi in più direzioni.
Quando un corpo si sposta sul piano traccia una traiettoria (rossa) in cui muta la direzione, il verso e la velocità.
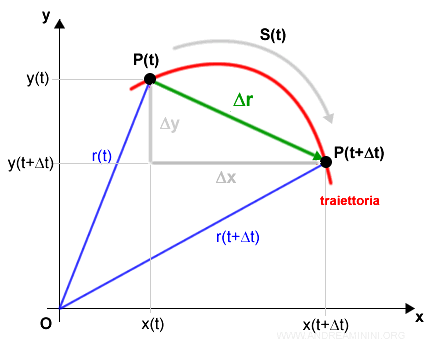
Il punto iniziale P(t) e il punto finale P(t+Δt) sono associati a due raggi vettori r(t) e r(t+Δt) di colore blu.
La differenza tra i due raggi vettori mi permette di calcolare il vettore spostamento Δr (verde).
$$ Δr = r(t+Δt) - r(t) $$
Grazie al vettore spostamento posso calcolare la velocità media vettoriale tra i due punti.
Nota. Si tratta comunque di un'approssimazione perché il modulo del vettore spostamento è lineare mentre la traiettoria è non lineare. Tuttavia, se l'intervallo di tempo è molto piccolo, il vettore fornisce una buona approssimazione della velocità media dello spostamento.
Facendo tendere l'intervallo temporale Δt a valori infinitesimali, ottengo la velocità istantanea del corpo nel punto iniziale t.
$$ \vec{v} = \lim_{Δt \rightarrow 0} \frac{Δr}{Δt} $$
Dal punto di vista geometrico il raggio vettore del punto finale si sposta a sinistra, avvicinandosi sempre più al punto iniziale.
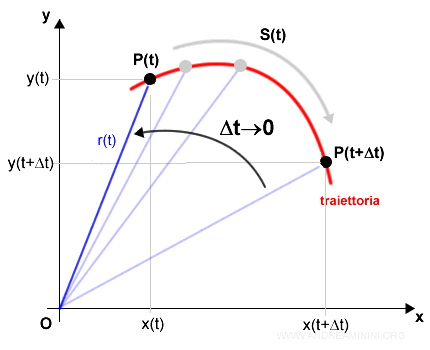
Poiché il vettore spostamento Δr è la differenza tra i due raggi vettori r(t+Δt) - r(t)
E' subito evidente che la velocità è la derivata del raggio vettore r(t) rispetto al tempo.
$$ \vec{v} = \lim_{Δt \rightarrow 0} \frac{r(t+Δt) - r(t)}{Δt} = \frac{d\vec{r}}{dt} $$
Detto in altri termini la velocità di spostamento è uguale alla derivata dello spazio percorso rispetto al tempo ds/dt nell'istante iniziale t.
$$ \vec{v} = \lim_{Δt \rightarrow 0} \frac{r(t+Δt) - r(t)}{Δt} = \frac{ds}{dt} = \dot{s} $$
Nota. In fisica la derivata di una funzione rispetto al tempo si indica anche con un'altra notazione più sintetica. Basta aggiungere un punto sopra la funzione per ogni ordine di derivazione. Ad esempio, la derivata prima è $$ \frac{ds}{dt} = \dot{s} $$ la derivata seconda è $$ \frac{d^2s}{dt} = \ddot{s} $$
Da un punto di vista geometrico, la derivata è uguale al coefficiente angolare della retta tangente nel punto P(t).
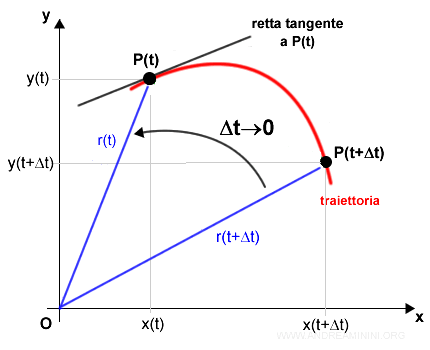
Più precisamente la tangente è un vettore velocità.
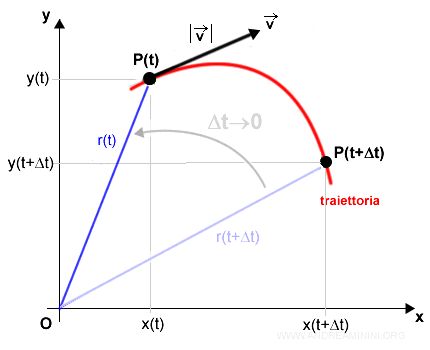
Questo mi permette di conoscere la direzione istantanea e la velocità istantanea del corpo nell'istante t.
Nota. Il modulo del vettore |v|, ossia la lunghezza del vettore, è la velocità istantanea del corpo nell'istante t.
Ripetendo lo stesso procedimento in alti punti della traiettoria, posso conoscere le velocità istantanee del corpo in ogni istante temporale (o posizione).
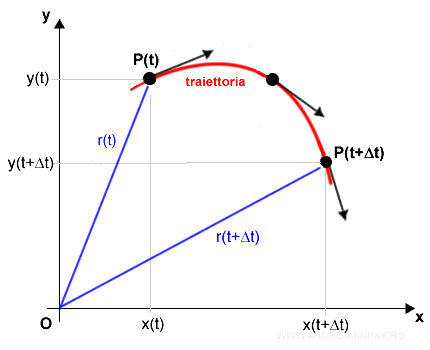
Considerando anche il verso di percorrenza la formula completa della velocità istantanea vettoriale diventa la seguente:
$$ \vec{v} = \frac{ds}{dt} \cdot u_T $$
Quest'ultima formula è anche detta velocità vettoriale perché individua il verso, la direzione e la velocità del punto.
Nota. Il versore uT indica la direzione dello spostamento del corpo verso destra (u=1) o sinistra (u=-1) sulla retta tangente alla traiettoria nel punto P(t). $$ dr = ds \cdot u_T $$
Il modulo della velocità vettoriale è, invece, la velocità istantanea del punto nell'istante t.
$$ v= \frac{ds}{dt} $$
Questo mi permette di trovare la velocità in un istante t a partire dalla posizione del corpo nello spazio.
Come trovare la posizione dalla velocità
Sapendo che la velocità istantanea nell'istante t è la derivata del raggio vettore r(t).
$$ v(t) = \frac{d \: r(t)}{d \: t} $$
L'integrale della velocità determina la posizione del punto a partire dalla velocità.
$$ \int_{t_0}^t v(t) \: dt = r(t) - r(t_0) $$
Metto in evidenza r(t) e diventa
$$ r(t) = r(t_0) - \int_{t_0}^t v(t) \: dt $$
A questo punto, basta calcolare l'integrazione rispetto ai moti componenti x,y per ottenere le coordinate sul piano.
Ovviamente, per farlo è necessario conoscere la posizione iniziale r(t0).
E così via.
