VelocitÓ media
Cos'è la velocità media
La velocità media misura la velocità dello spostamento di un corpo da una posizione iniziale S(t) a una posizione finale S(t+Δt) in un determinato periodo di tempo Δt=t2-t1. $$ v = \frac{S(t+Δt)-S(t)}{Δt} $$
In generale, la velocità media è una grandezza vettoriale perché da sola non descrive lo spostamento del corpo nello spazio.
Ad esempio, dire che un corpo si sposta a 100 m/s è inutile se non si specifica anche la direzione.
Nota. La velocità media può essere considerata una grandezza scalare soltanto nello spazio unidirezionale, perché in questo caso la direzione è nota a priori. Ad esempio sulla retta in uno spazio a una dimensione.
La velocità media in una retta
La velocità media in una retta è una grandezza scalare perché la direzione è già nota.
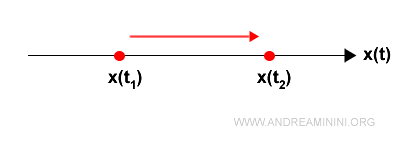
Per calcolarla prendo in considerazione la posizione del punto in una retta in due istanti di tempo t1 e t2
$$ x_1 = x(t_1) \\ x_2 = x(t_2) $$
Lo spazio percorso dal punto ΔS è la differenza tra le due posizioni
$$ ΔS = x(t_2) - x(t_1) $$
Nota. Il segno della differenza ΔS mi fornisce l'informazione sul verso del moto. Se ΔS>0 il punto si sposta verso destra. Viceversa, se ΔS<0 si sposta verso sinistra. Se ΔS=0 il punto è fermo in stato di quiete. Essendo una retta, In tutti i casi la direzione è nota ed è sempre la stessa.
L'intervallo temporale Δt è invece la differenza tra i due istanti temporali.
$$ Δt = t_2 - t_1 $$
Sapendo che la velocità media è il rapporto tra spazio percorso ΔS e l'intervallo di tempo Δt.
$$ v = \frac{S}{T} = \frac{ΔS}{Δt} = \frac{x(t+Δt)-x(t)}{Δt} $$
Nota. Durante il percorso il corpo può variare la velocità. Quest'ultima informazione non viene fornita dalla velocità media.
Posso rappresentare lo spostamento del corpo in un diagramma cartesiano ponendo lo spazio x sulle ordinate e il tempo t sulle ascisse.
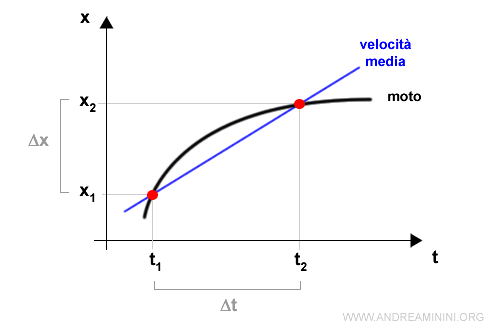
La velocità media è uguale al coefficiente angolare della retta secante (blu) alla posizione iniziale e finale.
La velocità media sul piano
La velocità media in uno spazio a due o più dimensioni è una grandezza vettoriale perché il corpo può spostarsi in tutte le direzioni.
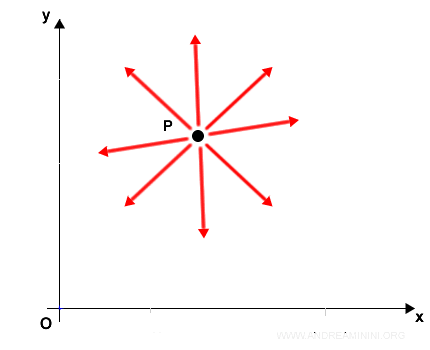
Pertanto, dire che il corpo si sposta a 100 m/s è inutile se non specifico anche la direzione.
Per farlo devo usare necessariamente un vettore.
Un esempio
In un intervallo di tempo Δt un punto materiale P si sposta sul piano dalla posizione iniziale P(t) alla posizione finale P(t+Δt)
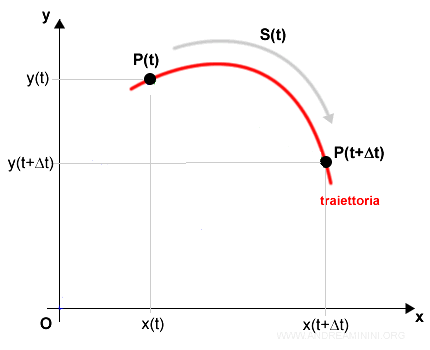
Nota. In questo diagramma gli assi misurano i moti componenti x e y. E' bene non confondersi con il diagramma del moto rettilineo dove le ascisse misurano il tempo.
Come si calcola la velocità media vettoriale?
Posso rappresentare la posizione iniziale P(t) e finale P(t+Δt) tramite due raggi vettori.
Il raggio vettore r(t) congiunge l'origine O con le coordinate della posizione iniziale (x(t),y(t)).
Il raggio vettore r(t+Δt) congiunge l'origine O con le coordinate della posizione finale x(t+Δt),y(t+Δt).
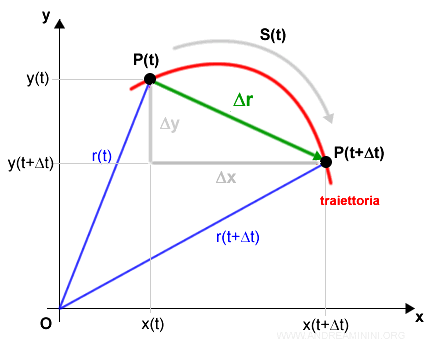
Il vettore Δr (verde) è detto vettore spostamento perché congiunge la posizione iniziale e verde.
E' uguale alla differenza tra i due raggi vettori.
$$ Δr = r(t+Δt)-r(t) $$
Nota. In questo caso Δr è una grandezza vettoriale ossia un vettore, perché è composto da una direzione, un verso e una lunghezza (modulo). Non è un numero scalare.
Pur non essendo uguale alla lunghezza della traiettoria (rosso), il modulo del vettore spostamento mi fornisce comunque un'approssimazione dello spazio percorso.
Questo mi permette di calcolare la velocità media come grandezza vettoriale tramite il rapporto incrementale Δr/Δt
$$ \vec{v} = \frac{Δr}{Δt} = \frac{r(t+Δt)-r(t)}{Δt} $$
Nota. La velocità media vettoriale non è uguale alla velocità effettiva del corpo perché la traiettoria S(t) non è lineare. E' solo una misura approssimativa "in linea d'aria" e per grandi distanze diventa fuorviante. Tuttavia, se lo spazio percorso è molto piccolo, fornisce una buona approssimazione della velocità media.
E così via.
