Le successioni convergenti
Una successione an è convergente se il limite della successione per n→∞ è un numero finito l $$ \lim_{n \rightarrow ∞} a_n = l $$ e per qualsiasi ε>0 esiste almeno un numero v tale che $$ l-ε < a_n < l+ε \:\:\: \forall n>v $$ 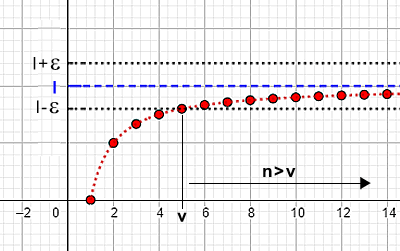
o in forma equivalente $$ | a_n - l | < ε \:\:\: \forall n>v $$
Tutte le successioni convergenti sono anche successioni limitate.
Non vale pero il contrario. Una successione limitata potrebbe non essere convergente.
Ad esempio la successione (-1)n oscilla tra -1 e +1. E' limitata ma non è convergente.
Nota. Se la successione converge a zero, la successione è detta successione infinitesima. E' un caso particolare di successione convergente. $$ \lim_{ n \rightarrow ∞ } a_n = 0 $$
Un esempio pratico
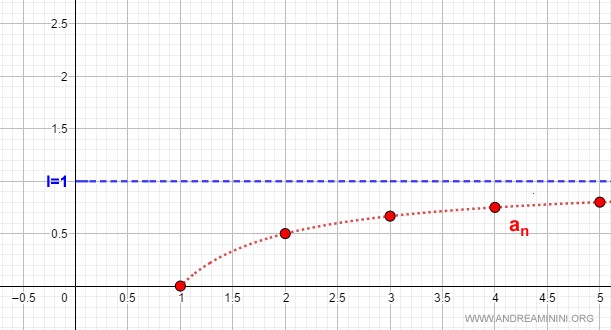
Prendo in considerazione la successione
$$ a_n = \frac{n-1}{n} $$
Il limite della successione per n→∞ è uguale a uno.
$$ \lim_{ n \rightarrow ∞ } \frac{n-1}{n} = 1 $$
Pertanto, la successione è convergente perché il limite per n→∞ è un numero finito.
Verifica
La successione è convergente se per qualsiasi ε >0 vale la diseguaglianza
$$ | a_n -l | <ε $$
In questo caso l=1
$$ | a_n -1 | <ε $$
La successione an è (n-1)/n
$$ | \frac{n-1}{n} -1 | <ε $$
Metto in evidenza n con qualche passaggio algebrico
$$ | \frac{n-1-n}{n} | <ε $$
$$ | \frac{1}{n} | <ε $$
Tolgo il modulo perché l'indice n>0
$$ \frac{1}{n} <ε $$
$$ \frac{1}{ε} <n $$
$$ n > \frac{1}{ε} $$
Quindi, se l'indice è maggiore di 1/ε, la differenza |an-l|<ε.
In questo caso il valore v è uguale a 1/ε.
$$ v= \frac{1}{ε} $$
Per ogni n>v la condizione |an-l|<ε è soddisfatta.
Questo dimostra che la successione è convergente.
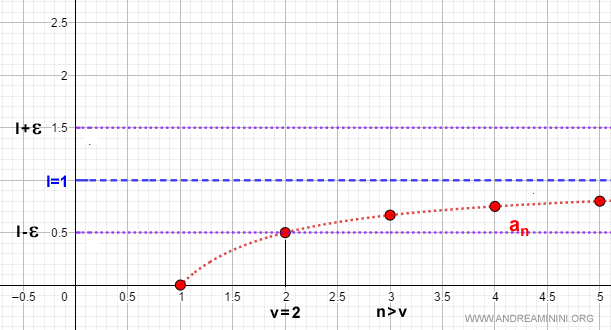
Nota. Nel grafico precedente ε=0.5 quindi v=1/ε è uguale a v=1/0.5=2. Per ogni indice n>v ossia n>2 la successione an è compresa nell'intorno (l-ε,l+ε).
E così via.
