Le successioni monotòne

Una successione è detta successione monotòna se si verifica una delle seguenti condizioni per ogni n ∈ N

• strettamente crescente
  se ogni termine è maggiore del precedente $$ a_{n+1} > a_n $$
• crescente
  se ogni termine è maggiore o uguale al precedente $$ a_{n+1} \ge a_n $$
• strettamente decrescente
  se ogni termine è minore del precedente $$ a_{n+1} < a_n $$
• decrescente
  se ogni termine è minore o uguale al precedente $$ a_{n+1} \le a_n $$

Le definizioni possono cambiare a seconda del testo di matematica.

Ad esempio, in alcuni libri le successioni crescenti/decrescenti sono dette crescenti/decrescenti in senso lato.

Nota. La successione è detta invece costante se ogni termine è uguale al precedente $$ a_{n+1} = a_n $$

Un esempio pratico

Esempio 1

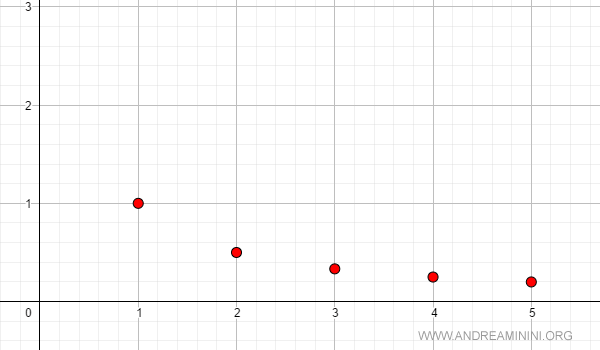
Questa successione è strettamente monotona decrescente

$$ a_n = \frac{1}{n} $$

perché per ogni n ∈ N

$$ a_{n+1} < a_n $$

$$ \frac{1}{n+1} < \frac{1}{n} $$

Ecco l'andamento della successione sul diagramma cartesiano.

Esempio 2

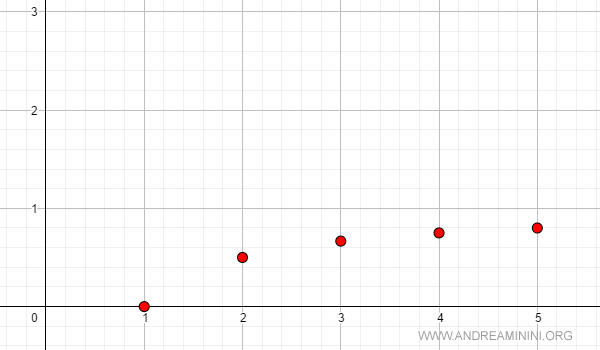
Questa successione è strettamente monotona crescente

$$ a_n = \frac{n-1}{n} $$

perché per ogni n ∈ N

$$ a_{n+1} > a_n $$

ossia

$$ \frac{n-1+1}{n+1} > \frac{n-1}{n} $$

$$ \frac{n}{n+1} > \frac{n-1}{n} $$

$$ \frac{1}{n(n+1)} > 0 $$

Ecco l'andamento grafico della successione

Le successioni costanti

Una successione è costante se per ogni n di N $$ a_{n+1} = a_n $$

Le successioni costanti sono un caso particolare delle successioni crescenti e decrescenti.

E così via.