Le successioni

Una successione è una funzione che associa ogni numero naturale n a un numero reale a_n. E' composta da una lista ordinata di oggetti numerabili a₁,...a_n detti termini della successione. $$\{ a_n \} = a_1, a_2, a_3, ... , a_n$$ Dove n è detto indice della successione, a_n è detto termine generico della successione.

Una successione è una funzione f nel dominio dei numeri naturali (N) e codominio nei numeri reali (R) o naturali (N) .

$$a: N \rightarrow R$$

Una successione può essere composta da un numero finito o infinito di termini.

$$\{ a_n \} = a_1, a_2, a_3, ... , a_n$$

Il termine a_n indica il termine ennesimo o termine generico della successione. Si legge "a con n".

A ogni termine della successione a₁, a₂, a₃,... è associata un'etichetta posta pedice in basso a destra rispetto alla lettera che indica la posizione dell'elemento nell'indice (lista).

Il termine a₁ è il primo termine della successione, il termine a₂ è il secondo termine e via dicendo

Nota. Le etichette dei termini della successione sono ordinate in senso crescente. Generalmente una successione comincia da n=1 oppure n=0. Tuttavia, posso anche definire un elemento iniziale n>1 maggiore di uno.

Un esempio di successione

Esempio 1

La successione 2n è la seguente:

$$a_n= 2n$$

I primi termini della successione sono

$$a_1 = 2 \cdot 1 = 2 \\ a_2 = 2 \cdot 2 = 4 \\ a_3 = 2 \cdot 3 = 6 \\ a_4 = 2 \cdot 4 = 8 \\ \vdots$$

Quindi, la successione è

$$\{ 2n \} = \ 2 \ , \ 4 \ , \ 6 \ , \ 8 \ , \ \dots$$

Esempio 2

La successione n² è la seguente:

$$a_n= n^2$$

I primi termini della successione sono

$$a_1 = 1^2 = 1 \\ a_2 = 2^2 = 4 \\ a_3 =3^2 = 9 \\ a_4 = 4^2 = 16 \\ \vdots$$

Quindi, la successione è

$$\{ n^2 \} = \ 1 \ , \ 4 \ , \ 9 \ , \ 16 \ , \ \dots$$

Esempio 3

La successione 1/n è la seguente:

$$a_n= \frac{1}{n}$$

I primi termini della successione sono

$$a_1 = \frac{1}{1} = 1 \\ a_2 = \frac{1}{2} \\ a_3 = \frac{1}{3} \\ a_4 = \frac{1}{4} \\ \vdots$$

Quindi, la successione è

$$\{ \frac{1}{n} \} = \ 1 \ , \ \frac{1}{2} \ , \ \frac{1}{3} \ , \ \frac{1}{4} \ , \ \dots$$

La rappresentazione delle successioni

Esistono diversi modi per rappresentare una successione

1] La rappresentazione per enumerazione

Una successione può essere rappresentata per enumerazione indicando i primi quattro o cinque termini della successione seguiti dai puntini.

$$2 \ , \ 4 \ , \ 9 \ , \ 16 \ \dots$$

La posizione dei termini nella lista indica l'indice della successione.

Nella successione precedente 2 è il primo termine della successione, 4 è il secondo termine e via dicendo.

Nota. Essendo i numeri naturali infiniti è impossibile descrivere tutti i termini della successione. Spesso i primi termini sono sufficienti per dedurre tutti gli altri termini successivi.

La rappresentazione per enumerazione è semplice ma non sempre evita le ambiguità.

Ad esempio, se due successioni diverse hanno i primi 4-5 termini uguali ma i restanti differenti. Quale delle due devo scegliere?

Inoltre, i primi termini potrebbero non far intuire facilmente il termine generico della successione.

Per evitare ogni dubbio, quando possibile è sempre preferibile indicare la successione tramite la rappresentazione analitica.

2] La rappresentazione analitica

Nella rappresentazione analitica esprimo la successione tramite il suo termine generico.

$$a_n = 2n-1$$

In questo modo si evita ogni dubbio.

Nota. Purtroppo non sempre è facile esprimere una successione tramite il suo termine generico.

3] La rappresentazione per ricorsione

Un altro modo per rappresentare la successione è la rappresentazione ricorsiva.

In questo caso ogni termine della successione è determinato dal termine precedente per ricorsione matematica.

Nella rappresentazione ricorsiva devo indicare

• il primo termine della successione (a₀)
• la relazione che lega il termine an al termine precedente a_n-1

Questo tipo di rappresentazione è molto utile nello studio dei sistemi complessi.

Esempio. Questa successione è rappresentata per ricorsione. $$\begin{cases} a_0 = 1 \\ \\ a_n = a_{n-1} + 2 \cdot n \end{cases}$$ In questo caso i primi termini della successione sono $$a_0 = 1$$ $$a_1 = a_0 + 2 \cdot 1 = 1 + 2 \cdot 1 = 3$$ $$a_2 = a_1 + 2 \cdot 2 = 3 + 2 \cdot 2 = 7$$ $$a_3 = a_2 + 2 \cdot 3 = 7 + 2 \cdot 3 = 13$$ Quindi i primi termini della successione sono $$1 \ , \ 3 \ , \ 7 \ , \ 13 \ , \ \dots$$

Successioni e prodotto cartesiano

Una successione ha il dominio nei numeri naturali N (o sottoinsieme di N) e il codominio S nei numeri naturali o reali. Pertanto, una successione è uguale al prodotto cartesiano NxS. $$(n, a_n )$$

Il primo elemento (n) della coppia è l'etichetta che indica la posizione dell'elemento nella successione.

Il secondo elemento (a_n) è il valore del termine n-esimo della successione.

Esempio

La successione {a_n} = 2n è la seguente:

$$a_1 = 2 \\ a_2 = 4 \\ a_3=6 \\ a_4 = 8$$

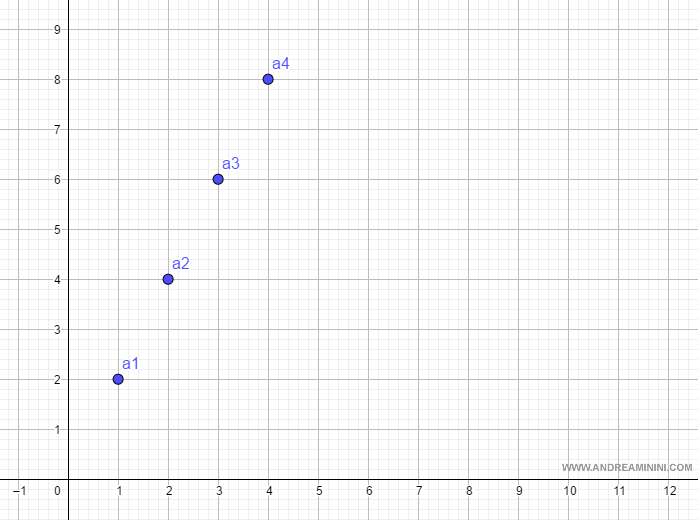
Il prodotto cartesiano (n, a_n) è il seguente:

$$( 1, 2 ) \\ ( 2,4) \\ (3,6) \\ (4,8)$$

La rappresentazione sul diagramma cartesiano rende tutto più chiaro

La differenza tra insieme e successione

In una successione l'ordine degli elementi è importante mentre in un insieme no.

Esempio

L'insieme A e B sono uguali, perché in un insieme la disposizione degli elementi non è significativa.

$$A = \{ 1, 2, 3, 4 \}$$

$$B = \{ 3, 1, 4, 2 \}$$

Viceversa, le successioni {a} e {b} sono diverse.

$$\{a\} = \{ 1, 2, 3, 4 \}$$

$$\{b\} = = \{ 3, 1, 4, 2 \}$$

Cosa sono le stringhe

Una successione con un numero finito di elementi è detta stringa.

Il numero degli elementi è detto lunghezza della stringa.

Esempio

Se n=4 la successione {a_n}=2n è detta stringa

$$a_1, a_2, a_3, a_4 = 2, 4, 6, 8$$

La lunghezza della stringa è uguale a 4.

E così via.