La successione divergente

Una successione a_n è detta divergente (o infinita) se il limite è uguale a +∞. $$ \lim_{ n \rightarrow +∞ } a_n = +∞ $$ se per qualsiasi M>0 esiste un numero naturale v tale che a_n>M per ogni n>v. $$ \forall M>0, \exists v : a_n>M \:\: \forall n>v $$

Allo stesso modo è detta divergente anche se il limite è uguale a -∞

Una successione a_n è detta divergente negativamente se il limite è uguale a -∞. $$ \lim_{ n \rightarrow +∞ } a_n = -∞ $$ se per qualsiasi M>0 esiste un numero naturale tale che a_n<-M per ogni n>v. $$ \forall M>0, \exists v : a_n<-M \:\: \forall n>v $$

Qualche esempio pratico

Esempio 1

La successione x²

$$ a_n = x^2 $$

è divergente positivamente perché il limite per n che tende a infinito è più infinito

$$ \lim_{n \rightarrow +∞} x^2 = +∞ $$

I primi termini della successione. $$ a_n = \{ 1, 4, 9, 16, ... , +∞ \} $$

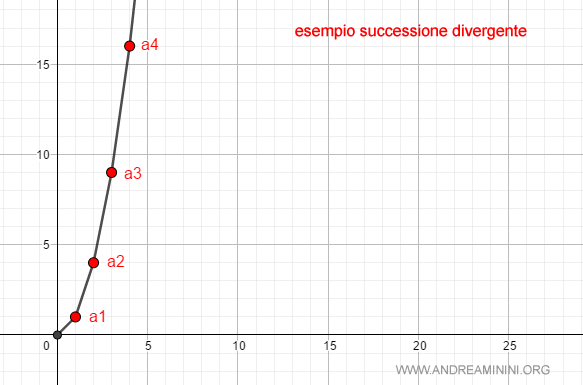
Se prendo il numero M=10 esiste il numero naturale v=3 (ossia a_v=a₃=9) tale che per ogni n>3 si ha a_n>10.

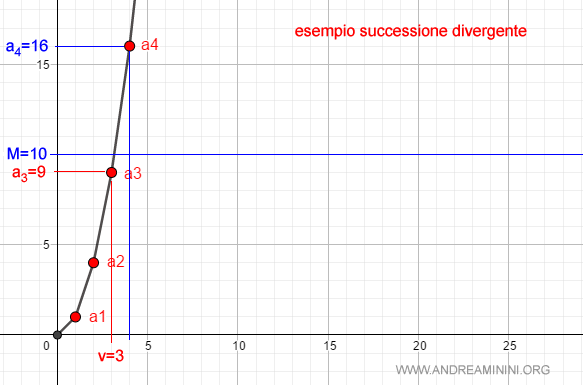
Lo stesso vale per qualsiasi altro numero M>0.

Esempio 2

La successione 1-x²

$$ a_n = 1-x^2 $$

è divergente negativamente perché il limite per n che tende a infinito è meno infinito.

$$ \lim_{n \rightarrow +∞} 1-x^2 = -∞ $$

I primi termini della successione. $$ a_n = \{ 0, -3, -8, -15, ... , -∞ \} $$

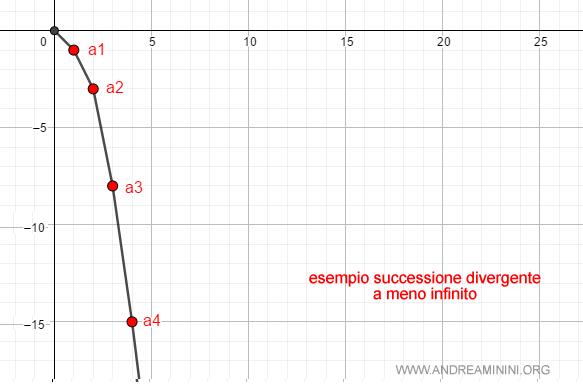
Se prendo il numero M=10 esiste il numero naturale v=3 (ossia a_v=a₃=-9) tale che per ogni n>3 si ha a_n<-M ossia a_n<-10.

Ad esempio, a₄=-15<-10

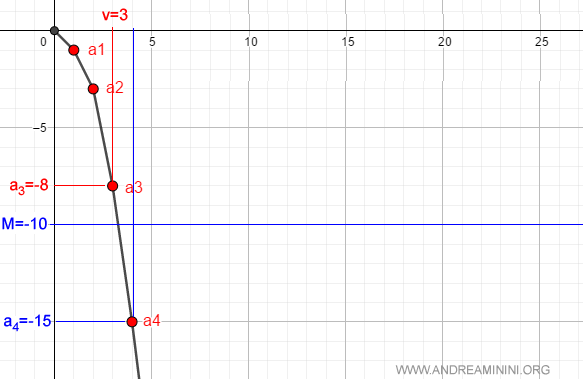
E così via.