Il postulato della divisibilità dei segmenti

Il postulato della divisibilità dei segmenti afferma che qualsiasi segmento di linea può essere diviso in un numero infinito di N segmenti più piccoli.

Dove N è un numero naturale qualsiasi.

Si tratta di un concetto fondamentale nella geometria euclidea ed è alla base di molte delle proprietà e dei teoremi in geometria.

Nota. In termini più formali, il postulato della divisibilità dei segmenti afferma che per ogni segmento AB e per ogni numero naturale n, esiste un punto C sul segmento AB tale che la lunghezza del segmento AB è n volte la lunghezza del segmento AC.

Un esempio pratico

Considero il segmento AB

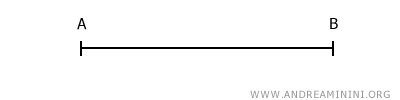
Qualunque sia la lunghezza del segmento AB, posso dividerla per n=2 e ottenere un punto C, tale che il segmento AB è due volte la lunghezza del segmento AB.

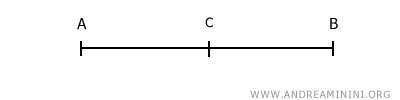
I segmenti AC e BC sono sottomultipli di AB e sono congruenti tra loro, ossia di uguale lunghezza tra loro.

Nota. In modo del tutto equivalente posso affermare che il segmento AC è 1/2 del segmento AB. E' la stesso concetto, visto da un altro punto di vista.

Allo stesso modo posso dividere il segmento in n=3 parti uguali.

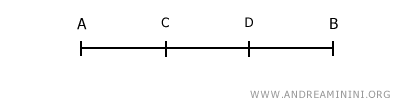
In questo caso il segmento AB è tre volte la lunghezza del segmento AC.

E via dicendo.