Teorema del trapezio isoscele
Nel trapezio isoscele gli angoli adiacenti a ciascuna base sono angoli congruenti.
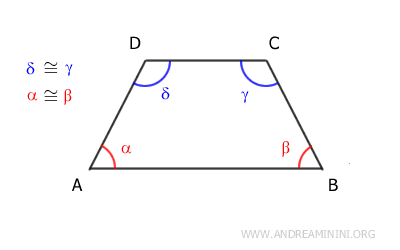
Ad esempio, nel trapezio isoscele ABCD gli angoli alfa e beta sono angoli congruenti perché sono gli angoli adiacenti alla base maggiore AB.
$$ \alpha \cong \beta $$
Allo stesso modo, gli angoli gamma e delta sono angoli congruenti, perché sono adiacenti alla base minore CD.
$$ \gamma \cong \delta $$
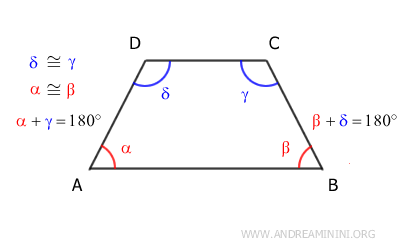
Corollario. In un trapezio isoscele gli angoli opposti sono supplementari, ossia la loro somma è pari a 180°. $$ \alpha + \gamma = 180° $$ $$ \beta + \delta = 180° $$
La dimostrazione
Considero un trapezio isoscele ABDC.
Essendo un trapezio isoscele, i lati obliqui sono congruenti AD≅CB e non paralleli.
Il trapezio isoscele posso scomporlo in tre figure: due triangoli rettangolo (ADE, BCF) e un quadrilatero, quadrato o rettangolo BCDE.
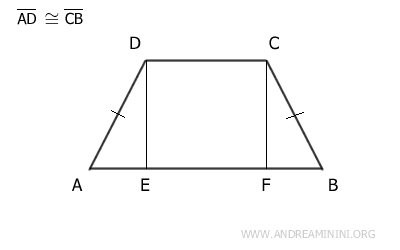
Il quadrilatero BCDE ha quattro angoli retti per definizione, indipendentemente dal fatto che si tratti di un rettangolo o di un quadrato.
Inoltre, i lati DE e CF del quadrilatero sono lati opposti, quindi sono congruenti DE≅CF.
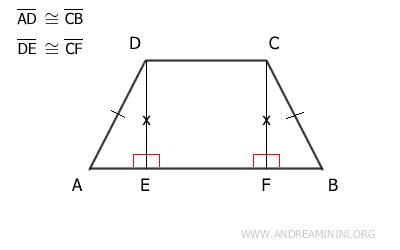
Per il criterio di congruenza dei triangoli rettangolo, i triangoli ADE e BCF sono congruenti (ADE≅BCF) perché hanno l'ipotenusa (AD≅CB) e un cateto congruenti (DE≅CF).
Quindi, essendo congruenti, i due triangoli ADE e BCF hanno gli angoli congruenti nello stesso ordine.
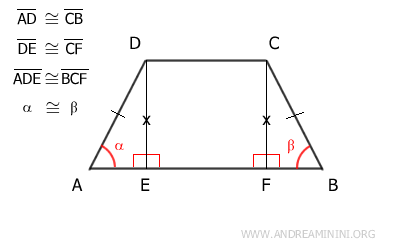
In particolar modo mi interessa sapere che gli angoli α≅β sono congruenti.
$$ \alpha = \beta $$
A questo punto applico il teorema delle rette parallele, considerando il lato AD come trasversale che interseca le rette parallele AB e CD.
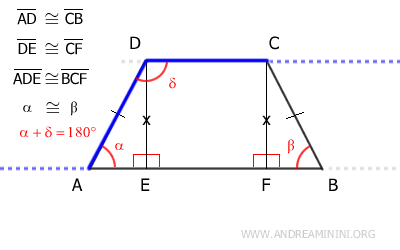
In base al teorema delle rette parallele gli angoli coniugati (alfa e delta) sono angoli supplementari (α+δ=180°), ossia la loro somma è pari a un angolo piatto.
$$ \alpha + \delta = 180° $$
Ora considero il lato BC come trasversale delle rette AB e CD.
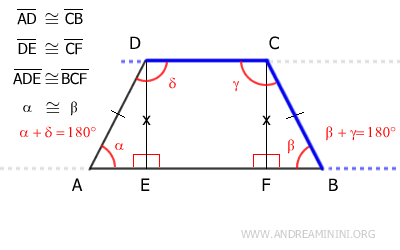
Per la stessa ragione, gli angoli coniugati beta e gamma sono angoli supplementari β+γ=180°.
$$ \beta + \gamma = 180° $$
Sapendo che α≅β deduco che anche gli angoli γ≅δ sono congruenti, perché sono gli angoli supplementari di due angoli congruenti.
$$ \alpha + \delta \cong \beta + \gamma = 180° $$
$$ \alpha + \delta \cong \beta + \gamma $$
$$ \alpha + \delta - \beta \cong \gamma $$
$$ \delta \cong \gamma $$
In conclusione gli angoli adiacenti a una base sono congruenti in un trapezio isoscele.
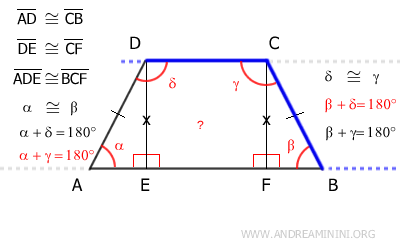
Di consequenza, sapendo che gli angoli adiacenti a un lato obliquo sono supplementari (180°), deduco che in un trapezio isoscele gli angoli opposti sono supplementari (α+γ=180° e β+δ=180°).
Teorema inverso del trapezio isoscele
Se un trapezio ha gli angoli adiacenti a una base congruenti, allora è un trapezio isoscele.
Dimostrazione
Per ipotesi iniziale considero un trapezio ABCD con gli angoli adiacenti a una base congruenti.
Ad esempio, gli angoli α≅β adiacenti alla base AB sono congruenti.
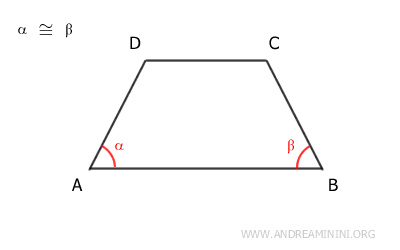
Non so ancora di quale tipo di trapezio si tratta... ma sicuramente so che le basi del trapezio sono parallele AB||CD tra loro.
Quindi, le altezze del trapezio DE e CF sono congruenti ossia DE≅CF e sono perpendicolari alle basi, quindi formano un angolo retto (90°) rispetto alla base AB.
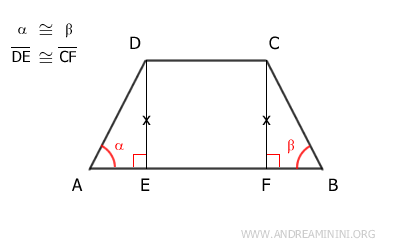
Le altezze delimitano due triangoli rettangolo ADE e BCF all'interno del trapezio.
I due triangoli ADE≅BCF sono congruenti per il secondo criterio di congruenza, perché hanno un lato congruente DE≅CF e due angoli congruenti α≅β e l'angolo retto (90°).
Quindi, i due triangoli congruenti ADE≅BCF hanno tutti i lati e gli angoli congruenti nello stesso ordine.
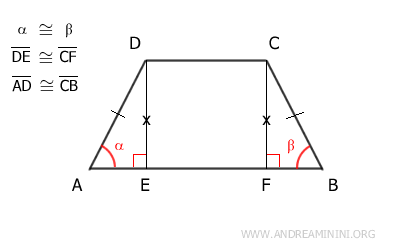
In questo caso mi interessa sapere che sono congruenti soprattutto le loro ipotenuse AD≅BC perché sono anche i lati obliqui del trapezio.
In conclusione, il trapezio ha i due lati obliqui congruenti AD≅BC. Quindi, è un trapezio isoscele.
E così via.
