Il teorema dei punti medi di un trapezio
Il segmento EF che collega i punti medi E e F dei lati obliqui di un trapezio è parallelo alle basi e ha una lunghezza uguale alla media delle due basi. $$ \overline{EF} = \frac{\overline{CD} + \overline{AB} }{2} $$
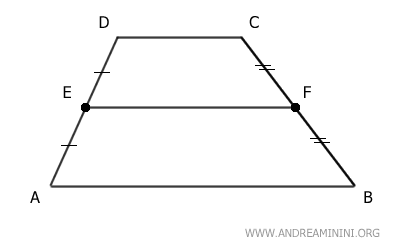
Un esempio pratico
Considero il trapezio ABCD.
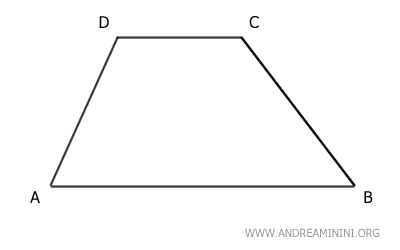
I lati obliqui AD e BC hanno rispettivamente i loro punti medi nei punti E e F.
Il segmento tra punti medi EF è parallelo alle basi AB e CD del trapezio.

Inoltre, la lunghezza del segmento EF è uguale alla semisomma delle due basi del trapezio (AB+CD)/2
$$ \overline{EF} = \frac{\overline{CD} + \overline{AB} }{2} $$
La dimostrazione
Considero un trapezio ABCD.

Il punto medio del lato obliquo AD è il punto E.
Essendo il punto medio, divide il lato AD in due segmenti congruenti AE≅DE .
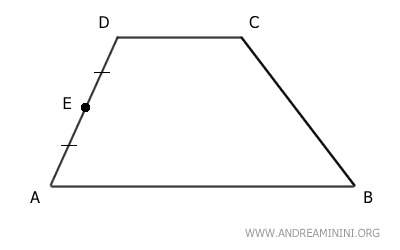
Traccio una retta r parallela alla base AB che passa per il punto medio E del lato AD.
Per il teorema del fascio di rette parallele, la retta r interseca il lato BC nel suo punto medio F che lo divide in due segmenti congruenti BF≅CF.
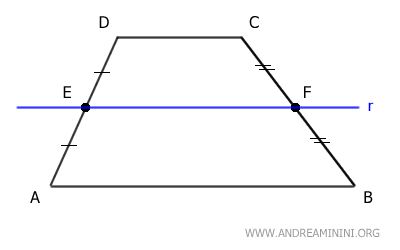
A questo punto considero il segmento EF tra i due punti medi dei lati obliqui AD e BC.

Ora traccio la diagonale AC che divide il trapezio in due triangoli e interseca il segmento EF nel punto G.
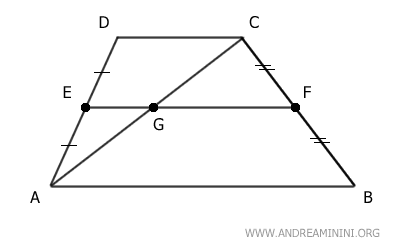
Analizzo il triangolo ACD.
Il segmento EG ha come estremo il punto medio E del lato AD ed è parallelo al lato CD del triangolo ACD.
Quindi, per il teorema dei punti medi del triangolo, il punto G è il punto medio del lato restante AC del triangolo e il segmento EG ha una lunghezza pari alla metà del lato parallelo CD.
$$ \overline{EG} = \frac{ \overline{CD} }{2} $$
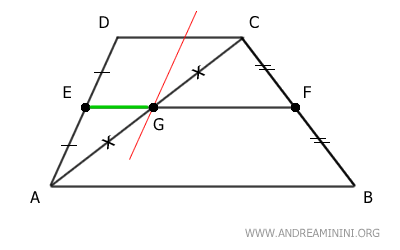
Analizzo il triangolo ABC.
Il segmento FG ha come estremi i punti medi G del lato AC e il punto medio F del lato BC del triangolo ABC.
Quindi, secondo il teorema dei punti medi del triangolo il segmento FG è parallelo e ha una lunghezza pari alla metà del lato restante AB.
$$ \overline{FG} = \frac{ \overline{AB} }{2} $$
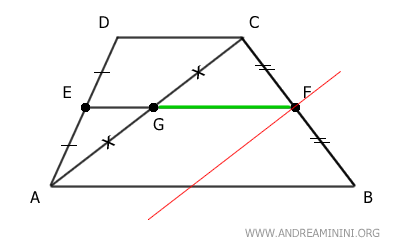
Ricapitolando, il segmento che congiunge i punti medi E e F dei lati obliqui del trapezio AD e BC è composto dai segmenti EG+FG
$$ \overline{EF} = \overline{EG} + \overline{FG} $$
Entrambi i segmenti EG e FG sono paralleli alle basi del trapezio AB e CD.
Quindi, il segmento EF è parallelo alle basi del trapezio.
Inoltre, sapendo che EG=CD/2 e FG=AB/2, la lunghezza del segmento EF è uguale alla semisomma (media) delle basi del trapezio.
$$ \overline{EF} = \overline{EG} + \overline{FG} = \frac{ \overline{CD} }{2} + \frac{ \overline{AB} }{2} = \frac{\overline{CD} + \overline{AB} }{2} $$
In questo modo il teorema dei punti medi di un trapezio è dimostrato.
E così via
