Area del rombo

L'area del rombo è data dal prodotto delle due diagonali diviso due $$ A = \frac{d_1 \cdot d_2}{2} $$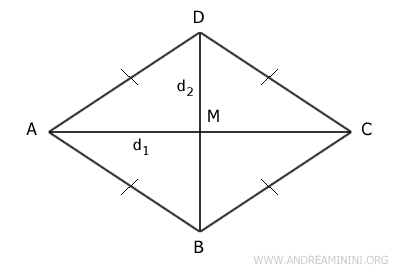

Questa formula deriva dal fatto che la superficie di un rombo equivale a quella di un triangolo rettangolo in cui la base e l'altezza sono congruenti alle diagonali del rombo.

Le formule inverse

Sapendo che l'area del rombo è

$$ A = \frac{d_1 \cdot d_2}{2} $$

posso calcolare una diagonale raddoppiando l'area del rombo e dividendola per l'altra diagonale

$$ d_1 = \frac{2A}{d_2} $$

$$ d_2 = \frac{2A}{d_1} $$

Un esempio pratico

Dato un rombo con diagonali di lunghezza d₁=3 cm e d₂=4, per calcolare l'area del rombo, utilizzo la formula:

$$ A = \frac{d_1 \cdot d_2}{2} $$

Sostituendo i valori delle diagonali forniti:

$$ A = \frac{3 \ cm \cdot 4 \ cm}{2} $$

$$ A = \frac{12 \ cm^2}{2} $$

$$ A = 6 \ cm^2 $$

Quindi, l'area del rombo è di 6 cm².

Dimostrazione

Considero un rombo ABCD.

Traccio le rette passanti per i vertici e perpendicolari alle diagonali.

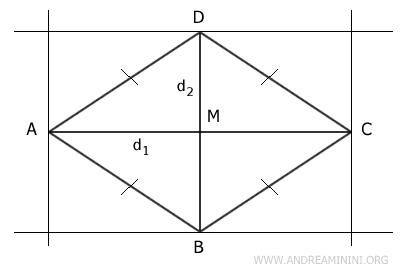
Le rette sono parallele e formano un rettangolo EFGI.

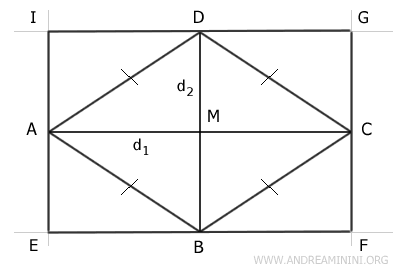
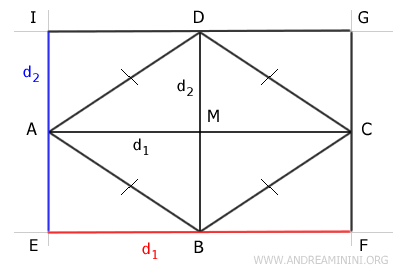
I lati del rettangolo sono congruenti alle diagonali del rombo.

$$ d_1 = \overline{AC} \cong \overline{EF} \cong \overline{GI} $$

$$ d_2 = \overline{BD} \cong \overline{EI} \cong \overline{FG} $$

Complessivamente, l'area del rettangolo è suddivisa in 8 triangoli congruenti, mentre quella del rombo da 4 triangoli congruenti.

Ne consegue che per conoscere l'area del rombo mi basta calcolare l'area del rettangolo, ossia base per altezza, e dividere il risultato per due.

In altre parole, l'area del rombo è equivalente alla metà dell'area del rettangolo.

$$ A = \frac{b \cdot h}{2} $$

Sapendo che i lati del rettangolo sono congruenti alle diagonali del rombo, b=d₁ e h=d₂, questo equivale a dire che bisogna moltiplicare le diagonali del rombo e dividere il prodotto per due.

$$ A = \frac{d_1 \cdot d_1}{2} $$

Questo spiega la formula usata per il calcolo dell'area di un rombo.

Osservazioni

Alcune osservazioni sull'area del rombo

• Il rombo è un parallelogramma con i lati congruenti. Quindi, la sua area può essere calcolata anche usando la formula dei parallelogrammi ossia base per altezza diviso due. $$ A = \frac{b \cdot h}{2} $$
• Il quadrato è un rombo con le diagonali congruenti. Quindi, l'area del quadrato posso calcolarla usando la formula del rombo $$ A = \frac{d \cdot d}{2} = \frac{d^2}{2} $$ Ne consegue la lunghezza diagonale del quadrato è $$ d^2 = 2A $$ applico la radice quadrata in entrambi i membri e ottengo $$ \sqrt{d^2}=\sqrt{2A} $$ $$ d=\sqrt{2A} $$

E così via.