Le proprietà del determinante

Il determinante di una matrice rispetta le seguenti proprietà:

1. Il determinante di una matrice trasposta det(A^T) è uguale al determinante della matrice det(A).
   

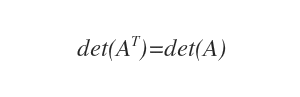
   Esempio. Nella seguente matrice la trasposizione non cambia il determinante.
   

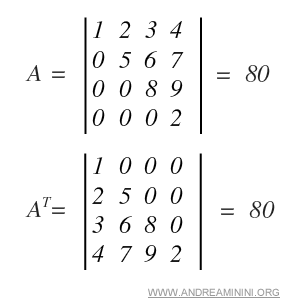
2. Se la matrice è triangolare inferiore o superiore, il determinante è uguale al prodotto degli elementi della diagonale principale.
   

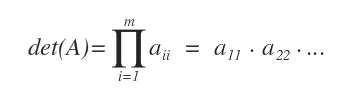
   Esempio. In questi casi il calcolo del determinante è molto più veloce.
   

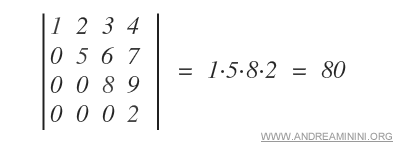
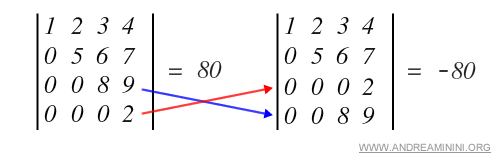
3. Scambiando due colonne o due righe tra loro, il determinante cambia di segno.

   Esempio.
   

4. Il prodotto di una colonna o riga per un numero scalare alfa (α), moltiplica per alfa anche il determinante det(αA).
   

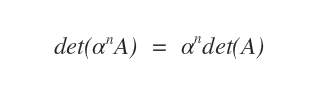
   Esempio. In questo esempio moltiplico la quarta riga R₄ per lo scalare 2. Anche il determinante della matrice viene moltiplicato per due.
   

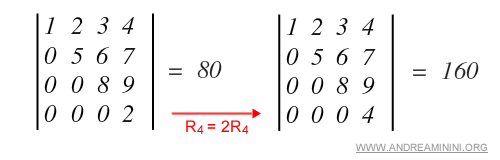
5. Il determinante non cambia di segno quando si somma una colonna con un multiplo di un'altra colonna. La stessa proprietà vale tra le righe.

   Esempio. In questo esempio sommo la quarta riga R₄ con la riga R₁ moltiplicata per due.
   

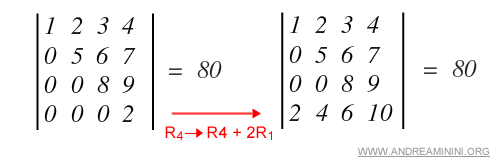
6. Il determinante di una matrice vale zero nei seguenti casi:
   
   a) una colonna o riga con tutti elementi nulli
   
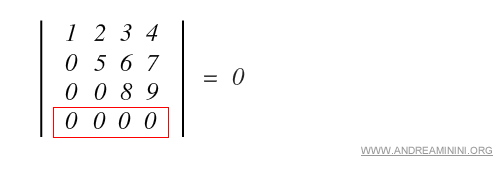
   b) due colonne o righe sono uguali
   
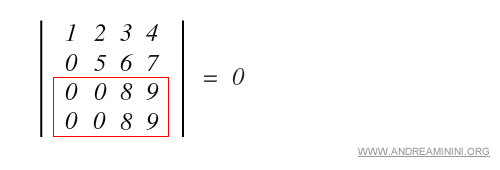
   c) due colonne o righe sono proporzionali
   

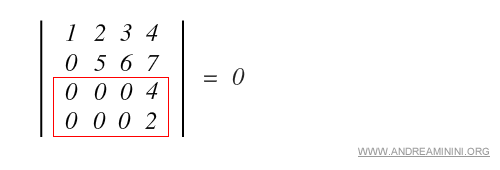
   Nota. Se una colonna o riga è uguale alla somma dei multipli di altre colonne e righe, le colonne o righe sono linearmente dipendenti. In caso di dipendenza lineare il determinante è nullo.

7. Il determinante del prodotto di due matrici det(AB) è uguale al prodotto dei determinanti delle matrici ( Teorema di Binet ).
   
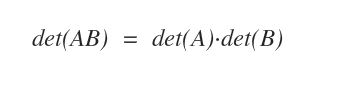
8. Il determinante della matrice inversa det(A^-1) è il reciproco del determinante di 1/det(A).
   

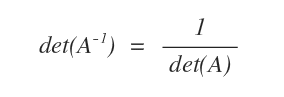
   Dimostrazione. Per il teorema di Binet il determinante di una matrice prodotto A·B è uguale al prodotto dei determinanti delle matrici det(A)·det(B) $$ det(A \cdot B) = det(A) \cdot det(B) $$ Quindi, il determinante del prodotto di una matrice invertibile A per la sua matrice inversa A^-1 è uguale al prodotto dei determinanti $$ det(A \cdot A^{-1}) = det(A^{-1} ) \cdot det(A) $$ Il prodotto di una matrice invertibile A per la matrice inversa A^-1 è il la matrice identità A·A^-1=I. Pertanto, il determinante det(AA^-1) è uguale al determinante det(I) $$ det(A \cdot A^{-1}) = det(A^{-1} ) \cdot det(A) = det(I) $$ Sapendo che il determinante della matrice identità è uguale a 1. $$ det(A \cdot A^{-1}) = det(A^{-1} ) \cdot det(A) = det(I) = 1 $$ anche il determinante della matrice invertibile per il determinante della matrice inversa è sempre uguale a 1. $$ det(A) \cdot det(A^{-1}) = 1 $$ $$ det(A^{-1}) = \frac{1}{det(A)} $$ Ho dimostrato la proprietà.

E così via.