Moto nel piano

Il moto nel piano è un moto che si svolge in uno spazio a due dimensioni.

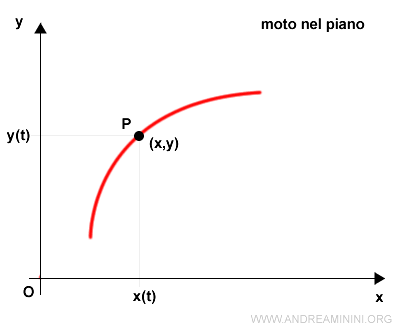
Legge oraria $$ r(t) = \vec{OP} = x(t) \cdot \vec{u_x} + y(t) \cdot \vec{u_y} $$ Velocità $$ \vec{v}(t) = \frac{d \vec{r}}{dt} = |v| \cdot \vec{u_T} $$ Accelerazione $$ \vec{a(t)} = \vec{a_T} + \vec{a_N} = \frac{d \ v}{dt} \vec{u_T} + \frac{v^2}{R} \cdot \vec{u_N} $$

Nel grafico precedente il tratto rosso è la traiettoria del corpo nel piano.

Qual è la differenza tra il moto piano e il moto rettilineo?

Nel moto rettilineo la direzione è unica. Può soltanto cambiare il verso e l'intensità del moto.

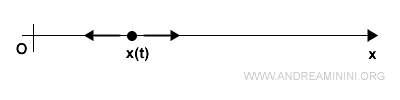
Nel moto piano, invece, la direzione può cambiare a 360° oltre al verso e all'intensità del moto.

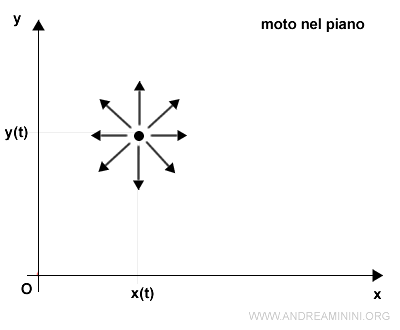
La legge oraria

Nel moto sul piano la posizione del punto materiale nello spazio è individuata dalle coordinate (x,y).

Quindi, la traiettoria del punto sul piano è una sequenza di coppie ( x(t) , y(t) ).

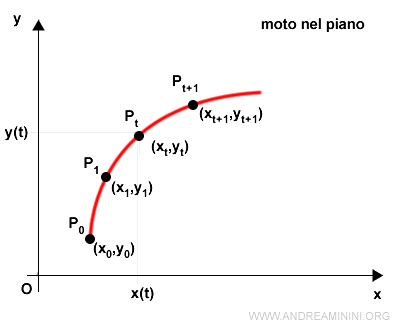
Pertanto la legge oraria è rappresentata da un sistema con due funzioni temporali.

$$ \begin{cases} x=x(t) \\ \\ y=y(t) \end{cases} $$

In alternativa, posso indicare la posizione del punto materiale sul piano anche tramite un raggio vettore r(t)

$$ r(t) = \vec{OP} $$

Dal punto di vista grafico il raggio vettore è un vettore applicato all'origine O verso il punto P.

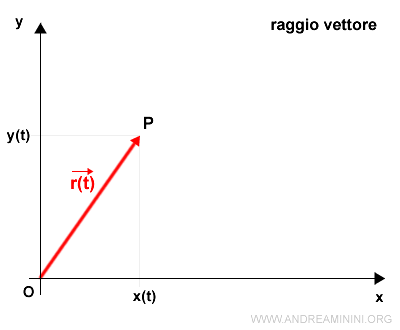
Dove il raggio vettore è una combinazione lineare delle funzioni x(t) e y(y) moltiplicate rispettivamente per i versori u_x e u_y.

$$ r(t) = \vec{OP} = x(t) \cdot \vec{u_x} + y(t) \cdot \vec{u_y} $$

Nota. Va specificato che il raggio vettore e i versori u_x e u_y sono grandezze vettoriali mentre x(y) e y(t) sono grandezze scalari (numeri).

Quindi, la traiettoria del punto sul piano può essere anche vista come una sequenza di raggi vettori r(t).

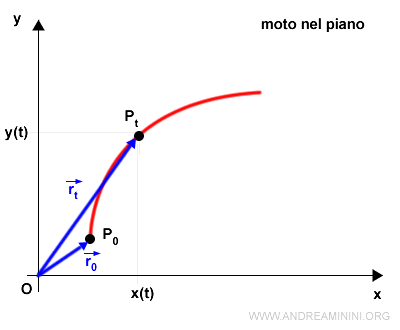
La velocità

Per misurare la velocità del punto materiale sul piano conviene usare la rappresentazione tramite il raggio vettore r(t).

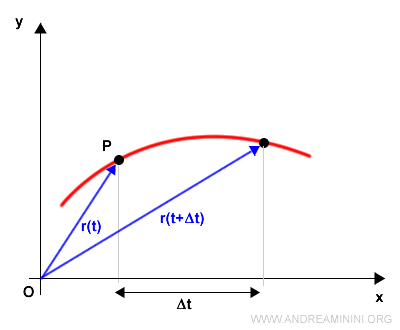
Date due posizioni nel tempo t e t+Δt

$$ r(t) $$

$$ r(t + \Delta t) $$

La velocità media del punto materiale è pari a

$$ \frac{\Delta \vec{r}}{ \Delta t} = \frac{\vec{r}(t+\Delta t) - \vec{r}(t)}{ \Delta t} $$

Dove differenza tra i due vettori è il vettore che congiunge i due punti.

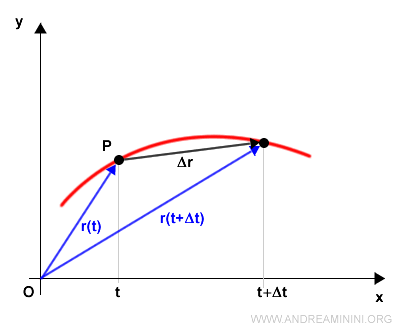
La frazione Δr/Δt è un rapporto incrementale.

Se faccio tendere a zero l'intervallo di tempo Δt→0 ottengo la derivata del raggio vettore rispetto al tempo.

$$ \lim_{\Delta t \rightarrow 0} = \frac{\Delta \vec{r}}{ \Delta t} = \lim_{\Delta t \rightarrow 0} = \frac{\vec{r}(t+\Delta t) - \vec{r}(t)}{ \Delta t} = \frac{d \vec{r}}{dt} $$

Pertanto, la velocità istantanea in un punto P del piano è uguale alla derivata del raggio vettore rispetto al tempo.

Dal punto di vista grafico la derivata dr/dt è il coefficiente angolare della retta tangente al punto P.

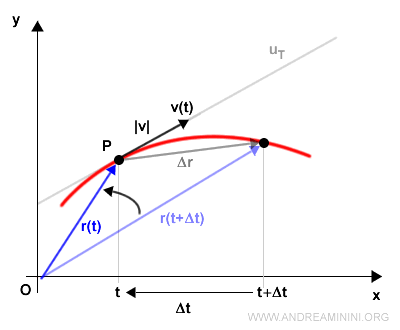
Nota. Il vettore della velocità istantanea posso indicarlo anche in questa forma equivalente tramite il prodotto tra il modulo (lunghezza) del vettore velocità |x| per il versore tangente al punto P. $$ \vec{v} = | \vec{v} | \cdot \vec{u_T} $$

Sia il modulo |v| che il versore u_T sono variabili nel corso del moto. Salvo nel caso in cui il punto si muova con velocità costante lungo una retta

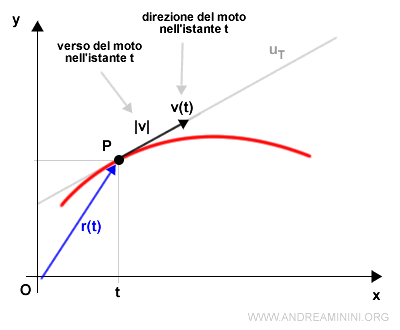
In ogni istante il vettore velocità v indica la direzione e il verso del moto.

Il modulo (lunghezza) del vettore velocità |v| indica, invece, l'intensità dello spostamento.

L'accelerazione

La formula dell'accelerazione di un punto materiale è la seguente $$ \vec{a(t)} = \frac{dv}{dt} \vec{u_T} + \frac{v^2}{R} \vec{u_N} $$ Dove u_N è il versore normale, u_T è il versore tangenziale, v è la velocità, R è il raggio di curvatura.

L'accelerazione è la derivata prima della velocità e la derivata seconda della legge oraria.

$$ \vec{a(t)} = \frac{d \vec{v}}{dt} = \frac{d^2 \vec{r}}{dt^2} $$

Tuttavia, nel piano la velocità può variare sia in modulo che nella direzione.

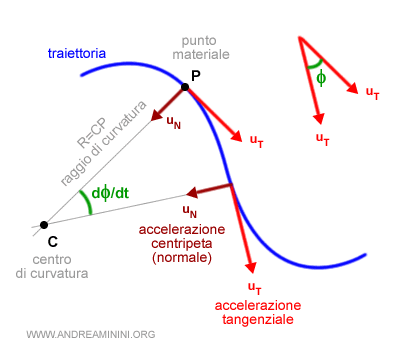
E' quindi utile suddividere l'accelerazione in due parti distinte tra loro:

• accelerazione normale (o centripeta)
  L'accelerazione normale descrive la variazione della direzione della velocità nel tempo. E' un vettore tangente alla traiettoria e diretto verso il centro della curva (centro di curvatura). L'accelerazione normale la indico con il simbolo a_N.
• accelerazione tangenziale
  L'accelerazione tangenziale descrive la variazione del modulo della velocità nel tempo. E' un vettore perpendicolare alla traiettoria e diretto verso il centro della curva. L'accelerazione tangenziale la indico con il simbolo a_T.

Nota. Il vettore dell'accelerazione normale e il vettore dell'accelerazione tangenziale sono vettori ortogonali perché formano sempre un angolo di 90° tra loro. Per un approfondimento sulla differenza tra accelerazione tangenziale e normale.

La somma dell'accelerazione normale e tangenziale determina l'accelerazione complessiva del punto materiale.

$$ \vec{a(t)} = \vec{a_T} + \vec{a_N} $$

Il vettore dell'accelerazione normale posso riscriverlo come il modulo di a_N per il versore u_N.

$$ \vec{a_N} = a_N \vec{u_N} = \frac{v^2}{R} u_N $$

Allo stesso modo il vettore dell'accelerazione tangenziale posso scriverlo come il modulo di a_T per il versore u_T.

$$ \vec{a_T} = a_T \vec{u_T} = \frac{dv}{dt} u_T $$

Quindi, l'accelerazione complessiva diventa

$$ \vec{a(t)} = \vec{a_T} + \vec{a_N} $$

$$ \vec{a(t)} = a_T \vec{u_T} + a_N \vec{u_N} $$

$$ \vec{a(t)} = \frac{dv}{dt} \vec{u_T} + \frac{v^2}{R} \vec{u_N} $$

Dimostrazione

L'accelerazione è la derivata della velocità.

$$ \vec{a(t)} = \frac{d \vec{v}}{dt} $$

Dal punto di vista grafico la velocità è un vettore tangente alla posizione del punto materiale sulla curva.

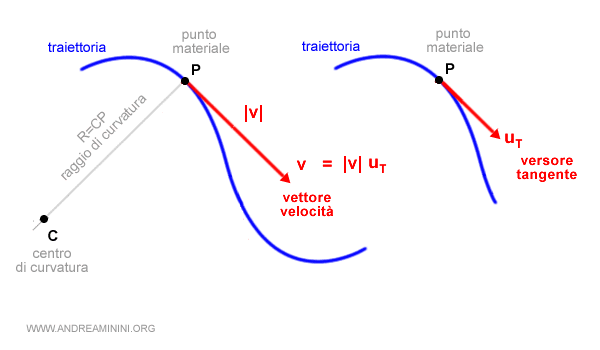
Quindi, posso riscrivere il vettore v come il prodotto tra il modulo di v per il versore tangente u_T ossia |v|·u_T.

$$ \vec{a(t)} = \frac{d (v \cdot \vec{u_T}) }{dt} $$

Calcolo la derivata del prodotto rispetto al tempo

$$ \vec{a(t)} = \frac{d \ v}{dt} \vec{u_T} + v \cdot \frac{d \ \vec{u_T}}{dt}$$

Nota. In questo caso sia la velocità v che il versore della direzione u_T variano nel tempo. Quindi sono entrambi derivabili per il tempo. Nessuno dei due termini è una costante.

E' già evidente che l'accelerazione è la somma di due vettori

Il primo vettore è l'accelerazione tangenziale a_T.

$$ \vec{a_T} = \frac{d \ v}{dt} \vec{u_T} $$

Ha la stessa direzione del vettore velocità perché dipende dal versore tangente u_T.

Il modulo del vettore a_T è determinato dalla derivata del vettore velocità nell'istante t.

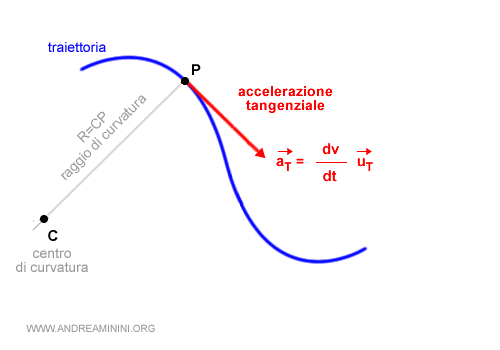
Il secondo termine è l'accelerazione normale a_N.

$$ a_N = v \cdot \frac{d \ \vec{u_T}}{dt} $$

Sapendo che la derivata di un versore è un versore ortogonale versore stesso (vedi dimostrazione).

$$ \frac{d \vec{u}}{dt} = \vec{v} \rightarrow \vec{v} \perp \vec{u} $$

Quindi la derivata del versore du_T/dt forma un angolo di 90° e si trova lungo la direzione normale del versore u_T.

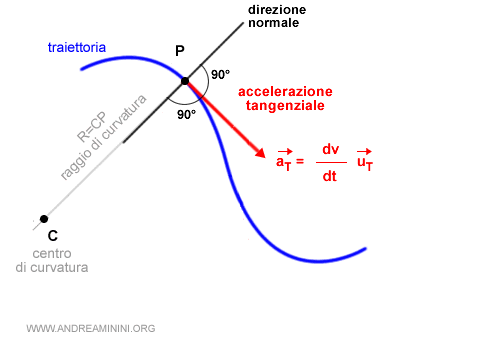
Ora devo cercare di studiare il moto sul piano come se fosse per un breve tratto un moto circolare.

Per farlo disegno un cerchio osculatore nella curva dove si trova il punto P che sto studiando.

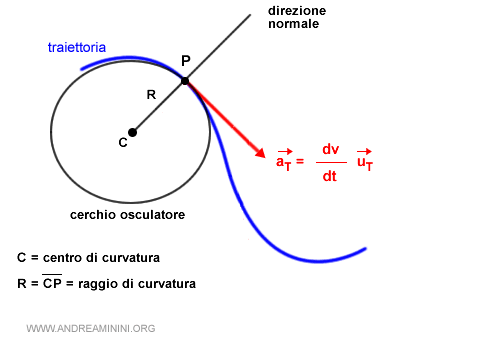
Cos'è il cerchio osculatore? E' una circonferenza che approssima la curva al meglio possibile. Esistono diversi cerchi osculatori contenuti dentro una curva. I cerchi più grandi sono quelli che la approssimano meglio. In genere un cerchio osculatore ha almeno tre punti in comune con la curva.

Il centro C del cerchio osculatore è detto centro di curvatura (o centro osculatore).

Il raggio R del cerchio osculatore è detto raggio di curvatura ed è uguale al segmento CP.

Studiando il cerchio osculatore trovo un'equivalenza tra il versore tangente u_T è il raggio di curvatura R.

Prendo due punti del moto P e P' lungo il cerchio osculatore. Questi punti hanno un versore tangente (u_T, u_T') e un raggio vettore (r₁,r₂).

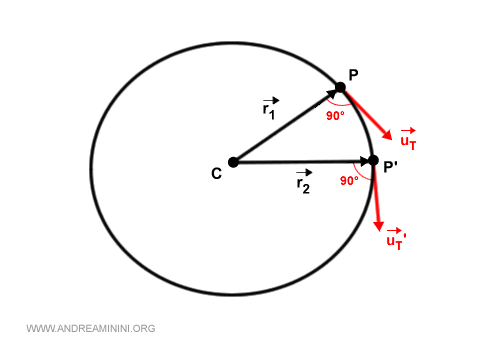
La differenza tra i due raggi vettore è il vettore spostamento Δr.

$$ \vec{\Delta r} = \vec{r_2} - \vec{r_1} $$

Geometricamente il vettore spostamento si presenta come la differenza tra i due versori.

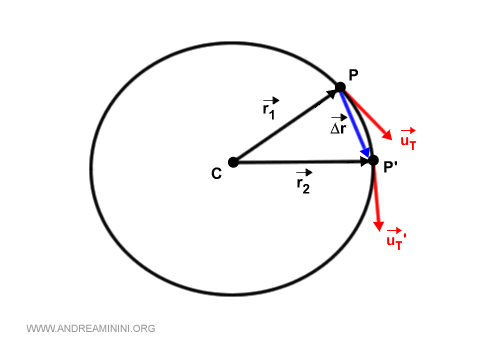
La differenza tra i due versori è il vettore Δu

$$ \vec{\Delta u} = \vec{u_T'} - \vec{u_T} $$

Il vettore Δu misura la variazione della direzione dei versori.

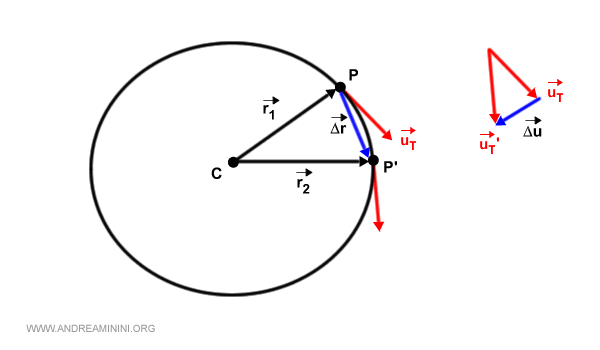
Si formano così due triangoli isoscele simili.

Il primo triangolo è composto dai vettori r₁, r₂, Δr.

Il secondo triangolo è composto dai vettori u_T, u_T', Δr.

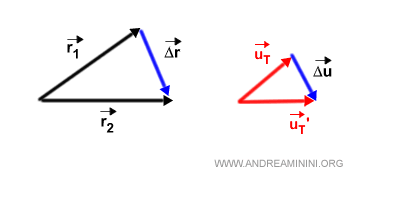
Nota. I due triangoli sono simili perché u_T è perpendicolare a r₁ e u_T' è perpendicolare a r₂. Sono triangoli isoscele perché u_T e u_T' sono uguali perché hanno entrambi modulo unitario. Anche r₁ e r₂ sono uguali perché sono entrambi pari al raggio del cerchio osculatore. Δr e Δu_T sono i lati incognita.

Quindi posso scrivere un'equivalenza tra le lunghezze dei lati dei triangoli (moduli dei vettori)

$$ \Delta u_T \ : \ u_T = \Delta r \ : \ r_1 $$

Metto in evidenza Δu_T.

$$ \Delta u_T = \frac{ \Delta r }{ r_1 } \cdot u_T $$

Sapendo che il modulo del versore u_T è 1

$$ \Delta u_T = \frac{ \Delta r }{ r_1 } \cdot 1 $$

$$ \Delta u_T = \frac{ \Delta r }{ r_1 } $$

Sapendo che la lunghezza del raggio r₁ è uguale al raggio di curvatura R ossia r₁=R.

$$ \Delta u_T = \frac{ \Delta r }{ R } $$

Faccio tendere Δr → 0 e ottengo la stessa equazione in termini infinitesimali

$$ d \ \ u_T = \frac{ d \ r }{ R } $$

$$ \frac{d \ \ u_T}{dt} = \frac{ d \ r }{ dt } \cdot \frac{1}{R} $$

In questo modo ho riscritto la derivata del versore tangente u_T in termini di vettore spostamento (r) e raggio di curvatura R.

Sostituisco du/dt nell'equazione dell'accelerazione.

$$ \vec{a(t)} = \frac{d \ v}{dt} \vec{u_T} + v \cdot \frac{d \ \vec{u_T}}{dt}$$

$$ \vec{a(t)} = \frac{d \ v}{dt} \vec{u_T} + v \cdot ( \frac{ d \ r }{ dt } \cdot \frac{1}{R} ) $$

La derivata del vettore spostamento è la velocità ossia dr/dt = v.

$$ \vec{a(t)} = \frac{d \ v}{dt} \vec{u_T} + v \cdot ( v \cdot \frac{1}{R} ) $$

$$ \vec{a(t)} = \frac{d \ v}{dt} \vec{u_T} + \frac{v^2}{R} $$

E infine aggiungo il versore u_N poiché so già che la derivata del versore du/dt si trova sulla direzione normale.

$$ \vec{a(t)} = \frac{d \ v}{dt} \vec{u_T} + \frac{v^2}{R} \cdot \vec{u_N} $$

Ho ottenuto la formula dell'accelerazione complessiva.

Dal punto di vista grafico

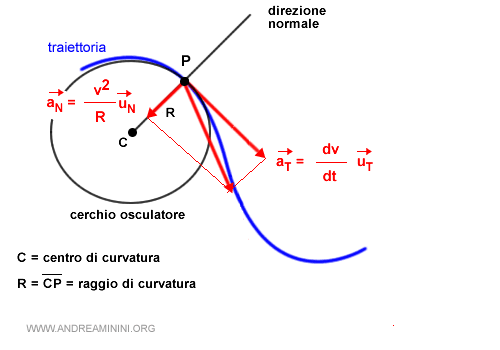
Sapendo che il vettore accelerazione è la somma vettoriale dell'accelerazione tangenziale e normale ossia a_T+a_N.

Dimostrazione alternativa. Per giungere alla stessa conclusione basta ricordarsi che in un moto circolare uniforme la derivata del versore u_T tangente alla circonferenza è la velocità angolare ω=dΦ/dt dove Φ è la variazione dell'angolo in un istante infinitesimo di tempo. $$ \frac{d \: u_T}{dt} = \frac{d \: Φ}{dt} \cdot u_N $$ La velocità angolare si trova su una direzione u_N (normale) ortogonale rispetto al versore u_T. Quindi il versore u_N è ortogonale al versore u_T. Infine, sapendo dalla trigonometria che un'angolo in radianti Φ=s/R è pari al rapporto tra l'arco (s) e il raggio (R), allora la derivata $$ \frac{d \: u_T}{dt} = \frac{dΦ}{dt} = \frac{d ( \frac{s}{R} ) }{dt} $$ Dove R è il raggio di curvatura ed è costante, quindi esce dalla derivata $$ \frac{d \: u_T}{dt} = \frac{dΦ}{dt} = \frac{d ( \frac{s}{R} ) }{dt} = \frac{1}{R} \cdot \frac{ds}{ dt } $$ La derivata dello spazio percorso è la velocità ds/dt=v. $$ \frac{d \: u_T}{dt} = \frac{dΦ}{dt} = \frac{d ( \frac{s}{R} ) }{dt} = \frac{1}{R} \cdot \frac{ds}{ dt } = \frac{1}{R} \cdot v = \frac{v}{R} $$ Sostituisco dΦ/dt=v e ottengo la formula finale. $$ \vec{a} = \frac{dv}{dt} \cdot u_T + v \cdot \frac{d \: u_T}{dt} $$ $$ \vec{a} = \frac{dv}{dt} \cdot u_T + v \cdot ( ( \frac{v}{R} ) \cdot u_N ) $$ $$ \vec{a} = \frac{dv}{dt} \cdot u_T + \frac{v^2}{R} \cdot u_N $$ Per un approfondimento è utile leggere anche gli appunti sulla differenza tra l'accelerazione tangenziale e centripeta.

E così via.