VelocitÓ angolare
La velocità angolare è un vettore ω con un modulo pari alla derivata della legge del moto angolare $$ |ω| = \frac{dθ}{dt} $$ la direzione coincide con l'asse di rotazione ed è perpendicolare al piano in cui si trova la circonferenza (moto del corpo) mentre il verso è tale che dall'estremo del vettore w il moto del corpo appaia in senso antiorario.
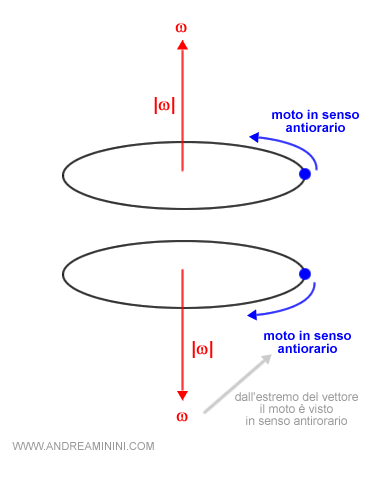
Generalmente la velocità angolare è una retta ortogonale al piano del moto che passa per il centro della circonferenza.
Come si misura la velocità angolare
Per misurare la velocità angolare (grandezza scalare |ω|) di un moto circolare si utilizza l'intera circonferenza (Δθ=2π) ossia un angolo giro.
$$ ω = \frac{Δθ}{t} = \frac{2π}{t} $$
Pertanto, il tempo (t) coincide con il periodo T del moto circolare.
$$ ω = \frac{2π}{T} $$
Essendo la frequenza (f) l'inverso del periodo (f=1/T) la formula precedente posso anche scriverla in questa forma
$$ ω = 2πf $$
Ho così trovato il modulo |ω| del vettore ω.
Facendo l'analisi dimensionale della formula si comprende il fatto che la velocità angolare è misurata in radianti/secondi (rad/s).
Dimostrazione. L'angolo giro (2π) è una grandezza misurata in radianti [rad] o in gradi. La frequenza (f) è l'inverso del periodo (1/T) che, a sua volta, si misura in tempo [T-1]. Pertanto, la dimensione della formula 2π/T è [rad][T-1] ossia radianti al secondo.
La differenza tra velocità angolare e la velocità
La velocità angolare (ω) misura la velocità con cui varia l'angolo θ(t) in un moto circolare.
Si distingue dalla velocità (v) che, invece, misura la velocità del corpo a percorrere uno spazio S sulla traiettoria (circonferenza).
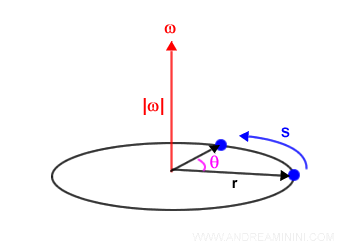
Tra il vettore della velocità angolare (ω), il vettore della velocità (v) e il raggio vettore (r) c'è una stretta relazione.
$$ v = ω \: x \: r $$
Dimostrazione. La formula della velocità è uguale allo spazio (s) percorso sulla circonferenza fratto il tempo (t). $$ v= \frac{s}{t} $$ L'arco percorso è uguale al modulo del vettore raggio |r| per l'angolo θ. $$ s = |r| \cdot θ $$ Quindi, posso riscrivere la velocità come. $$ v = \frac{s}{t} = \frac{|r| \cdot θ}{t} $$ Il rapporto tra l'angolo e il tempo è la velocità angolare. $$ ω = \frac{θ}{t} $$ Pertanto, il rapporto tra la velocità (v) e la velocità angolare (ω) è $$ v = ω \cdot |r| $$ Ponendo R=|r| $$ v = w \cdot R $$
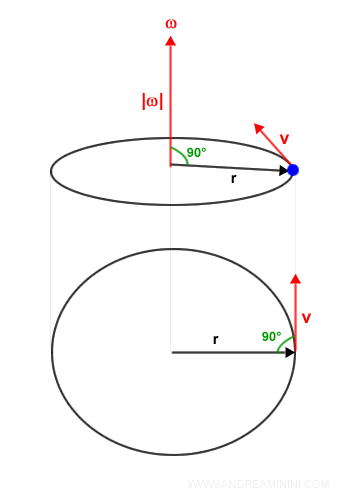
vettori ω,w e r sono vettori ortogonali tra loro perché presi a coppia formano sempre un angolo di 90° (π/2).
L'accelerazione angolare
L'accelerazione angolare è la derivata della velocità angolare. $$ α = \frac{d \: ω}{dt} $$
Si misura in radianti al secondo quadro (rad/s2).
La ragione è molto semplice.
A sua volta la velocità angolare è la derivata della legge oraria angolare.
$$ ω = \frac{d \: θ}{dt} $$
Pertanto, l'accelerazione angolare è la derivata seconda della legge oraria angolare.
$$ α = \frac{d \: ω}{dt} = \frac{d^2 \: θ}{dt^2} $$
Facendo una rapida analisi dimensionale, l'angolo si misura in radianti mentre il tempo al quadrato in secondi.
$$ α = \frac{d^2 \: θ}{dt^2} = \frac{[Rad]}{[T^2]} = [Rad] \cdot [T^{-2}] $$
E così via
