Il lancio di un grave

In fisica, il concetto di "lancio di un grave" è il movimento di un oggetto che viene lanciato verso l'alto e subisce l'azione della forza di gravità lungo il suo percorso. Durante il moto l'oggetto segue una traiettoria a forma di parabola.

L'oggetto viene inizialmente accelerato verso l'alto, contrapponendosi alla forza di gravità.

Una volta che l'oggetto raggiunge l'altezza massima, la sua velocità si riduce a zero e poi inizia a cadere verso il basso sotto l'effetto della forza di gravità.

La traiettoria dell'oggetto dipende dalla velocità iniziale del lancio (v₀), dall'angolo di lancio (α) e dall'accelerazione di gravità (g=9,8 m/s²).

Questo è il sistema che descrive il moto (x;y) in funzione del tempo (t)

$$ \begin{cases} x = x_0 + v_0 \cdot \cos( \alpha ) \cdot t \\ \\ y = y_0 + v_{0} \cdot \sin( \alpha ) \cdot t - \frac{1}{2} g \cdot t^2\end{cases} $$

Dal sistema posso anche ottenere la posizione di y in funzione di x.

$$ y = y_0 + \tan( \alpha ) \cdot (x - x_0) - \frac{1}{2} \cdot g \cdot (x - x_0)^2 \cdot \frac{1}{v_0^2 \cdot \cos^2( \alpha )} $$

Nell'ipotesi semplificatrice in cui la posizione iniziale è x₀=0 e y₀=0.

$$ y = \tan( \alpha ) \cdot x - \frac{1}{2} \cdot g \cdot x^2 \cdot \frac{1}{v_0^2 \cdot \cos^2( \alpha ) } $$

Utilizzando le equazioni del moto parabolico, posso calcolare la distanza percorsa (gittata), l'altezza massima raggiunta e il tempo di volo dell'oggetto durante il lancio.

L'altezza massima (h) del lancio si ottiene usando questa formula

$$ h = y_0 + \frac{1}{2} \cdot \frac{v_0^2 \sin^2 (\alpha) }{g} $$

La gittata (G) la ottengo, invece, utilizzando quest'altra formula

$$ x = \frac{v_0^2 \cdot \sin (2\alpha)}{g} $$

Il tempo di volo (t) dal lancio all'impatto è

$$ t = \frac{2 \cdot v_{0} \cdot \sin( \alpha ) }{g} $$

Nota. Il lancio di un grave è un esempio comune ed è utilizzato in fisica per comprendere i principi del moto dei corpi sotto l'influenza della gravità. È un concetto fondamentale nello studio della cinematica e della meccanica classica.

Come si calcola la traiettoria

Per studiare la traiettoria dell'oggetto nel lancio di un grave devo considerare uno spazio in due dimensioni (x;y) dove x è la lunghezza mentre y è l'altezza.

Nella cinematica si considera l'oggetto come un punto materiale privo di massa.

Quindi, in questi calcoli non devo preoccuparmi della massa dell'oggetto, né della sua forma.

In generale il lancio può avvenire con un angolo da 0° a 90° ossia da 0 a π/2 radianti.

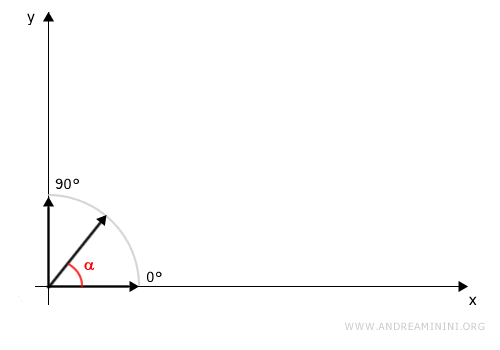
In qualsiasi caso il vettore del lancio si può suddividere in due componenti x e y.

Ogni componente è la proiezione del vettore sugli assi cartesiani.

Per ipotesi considero che non ci sia nessun ostacolo a fermare moto in orizzontale. Quindi, nessun vento o attrito da parte dell'aria.

Nel moto verticale, invece, considero la forza di gravità (g=9,8 m/s²) che attira il corpo verso il basso.

$$ \begin{cases} a_x = 0 \\ \\ a_y = - g \end{cases} $$

Nota. L'accelerazione sull'asse x è nulla (ax=0) perché non c'è alcuna forza ad accelerare o decelerare il moto sull'asse orizzontale. L'accelerazione sull'asse y è, invece, negativa (a_y=-g) perché la forza di gravità agisce in senso opposto rispetto al versore dell'asse y. La freccia y del diagramma cartesiano va verso l'alto mentre la forza di gravità (g) attira il corpo verso il basso.

Sapendo che l'accelerazione è la derivata prima della velocità rispetto al tempo, posso ricavare la velocità tramite un'operazione di integrazione dell'accelerazione.

$$ \begin{cases} v_x = \int a_x \ dt \\ \\ v_y = \int a_y \ dt \end{cases} $$

$$ \begin{cases} v_x = v_{0x} + a_x \cdot t \\ \\ v_y = v_{0y} + a_y \cdot t \end{cases} $$

Dove v_0x e v_0y sono le velocità iniziali sull'asse x e y. Sono le costanti degli integrale.

Sostituisco a_x=0 e a_y=-g

$$ \begin{cases} v_x = v_{0x} + 0 \cdot t \\ \\ v_y = v_{0y} + (- g) \cdot t \end{cases} $$

$$ \begin{cases} v_x = v_{0x} \\ \\ v_y = v_{0y} - g \cdot t \end{cases} $$

Sapendo che la velocità è la derivata della legge del moto, posso ricavare la legge del moto sulle coordinate (x;y) tramite l'integrazione delle equazioni della velocità

$$ \begin{cases} x = \int v_x \ dt \\ \\ y = \int v_y \ dt \end{cases} $$

In questo caso v_x=v_0x e v_y=v_0y - gt

$$ \begin{cases} x = \int v_{0x} \ dt \\ \\ y = \int v_{0y} - g \cdot t \ dt \end{cases} $$

A questo punto applico una semplice regola della trigonometria.

Le componenti della velocità v_0x e v_0y sono le proiezioni del vettore velocità v sugli assi cartesiani e il vettore velocità ha una lunghezza (modulo) pari alla velocità iniziale v₀.

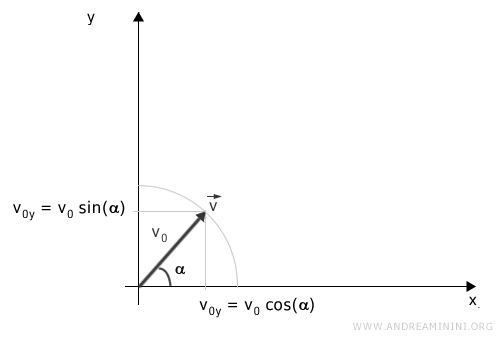
Quindi, posso scrivere le componenti v_0x e v_0y come il modulo del vettore velocità moltiplicato per il coseno e il seno dell'angolo di lancio.

Pertanto, v_0x=v₀·cos(α) e v_0y=v₀·sin(α)

$$ \begin{cases} x = \int v_0 \cdot \cos( \alpha ) \ dt \\ \\ y = \int v_{0} \cdot \sin( \alpha ) - g \cdot t \ dt \end{cases} $$

A questo punto calcolo gli integrali.

$$ \begin{cases} x = v_0 \cdot \cos( \alpha ) \cdot t + x_0 \\ \\ y = \int v_{0} \cdot \sin( \alpha ) \ dt - \int g \cdot t \ dt \end{cases} $$

$$ \begin{cases} x = v_0 \cdot \cos( \alpha ) \cdot t + x_0 \\ \\ y = v_{0} \cdot \sin( \alpha ) \cdot t + y_0 - \int g \cdot t \ dt \end{cases} $$

$$ \begin{cases} x = v_0 \cdot \cos( \alpha ) \cdot t + x_0 \\ \\ y = v_{0} \cdot \sin( \alpha ) \cdot t + y_0 - \frac{1}{2} g \cdot t^2\end{cases} $$

Ho trovato le equazioni del moto del lancio del grave che mi permettono di calcolare la traiettoria dell'oggetto nel tempo.

$$ \begin{cases} x = x_0 + v_0 \cdot \cos( \alpha ) \cdot t \\ \\ y = y_0 + v_{0} \cdot \sin( \alpha ) \cdot t - \frac{1}{2} g \cdot t^2\end{cases} $$

Si tratta di un moto uniformemente accelerato.

A questo punto ricavo la variabile t nella prima equazione.

$$ \begin{cases} t = \frac{x - x_0}{v_0 \cdot \cos( \alpha )} \\ \\ y = y_0 + v_{0} \cdot \sin( \alpha ) \cdot t - \frac{1}{2} \cdot g \cdot t^2\end{cases} $$

Poi sostituisco la variabile t nella seconda equazione.

$$ \begin{cases} t = \frac{x - x_0}{v_0 \cdot \cos( \alpha )} \\ \\ y = y_0 + v_{0} \cdot \sin( \alpha ) \cdot \frac{x - x_0}{v_0 \cdot \cos( \alpha )} - \frac{1}{2} \cdot g \cdot (\frac{x - x_0}{v_0 \cdot \cos( \alpha )})^2\end{cases} $$

$$ \begin{cases} t = \frac{x - x_0}{v_0 \cdot \cos( \alpha )} \\ \\ y = y_0 + v_{0} \cdot \frac{ \sin( \alpha ) }{ \cos( \alpha ) } \cdot \frac{x - x_0}{v_0} - \frac{1}{2} \cdot g \cdot \frac{(x - x_0)^2}{v_0^2 \cdot \cos^2( \alpha )}\end{cases} $$

$$ \require{cancel} \begin{cases} t = \frac{x - x_0}{v_0 \cdot \cos( \alpha )} \\ \\ y = y_0 + \cancel{v_{0}} \cdot \frac{ \sin( \alpha ) }{ \cos( \alpha ) } \cdot \frac{x - x_0}{\cancel{v_0}} - \frac{1}{2} \cdot g \cdot \frac{(x - x_0)^2}{v_0^2 \cdot \cos^2( \alpha )}\end{cases} $$

Sapendo che sin(α)/cos(α)=tan(α) per la seconda relazione fondamentale della trigonometria.

$$ \begin{cases} t = \frac{x - x_0}{v_0 \cdot \cos( \alpha )} \\ \\ y = y_0 + \tan( \alpha ) \cdot (x - x_0) - \frac{1}{2} \cdot g \cdot (x - x_0)^2 \cdot \frac{1}{v_0^2 \cdot \cos^2( \alpha )}\end{cases} $$

Quindi, la traiettoria della legge del moto è è una parabola.

$$ y = y_0 + \tan( \alpha ) \cdot (x - x_0) - \frac{1}{2} \cdot g \cdot (x - x_0)^2 \cdot \frac{1}{v_0^2 \cdot \cos^2( \alpha )} $$

Nell'ipotesi semplificatrice in cui la posizione iniziale è x₀=0 e y₀=0.

$$ y = \tan( \alpha ) \cdot x - \frac{1}{2} \cdot g \cdot x^2 \cdot \frac{1}{v_0^2 \cdot \cos^2( \alpha ) } $$

L'altezza massima del lancio

La formula per trovare l'altezza massima del lancio di un grave è $$ h = y_0 + \frac{1}{2} \cdot \frac{v_0^2 \sin^2 \alpha }{g} $$

Questa formula calcola quanto lontano cadrà l'oggetto.

Dimostrazione

Quando il corpo raggiunge l'altezza massima, la componente verticale della velocità è uguale a zero, ossia v_y=0

In questo punto il corpo manifesta anche un'inversione di velocità sull'asse y.

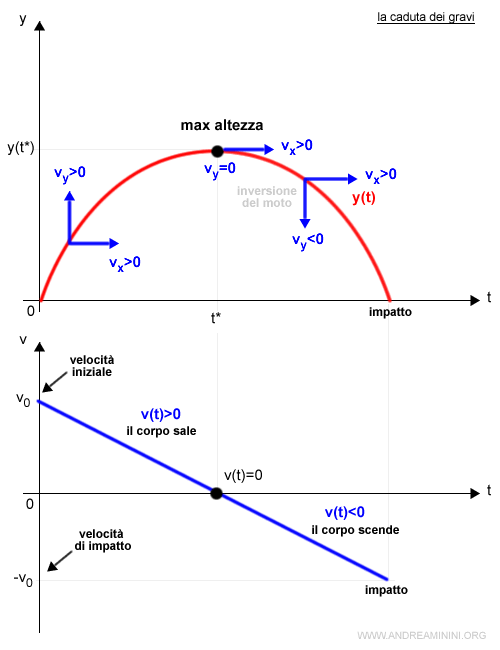
Pertanto, per prima cosa riprendo la scomposizione della velocità nelle sue componenti x e y già vista nel paragrafo precedente

$$ \begin{cases} v_x = v_{0} \cdot \cos \alpha \\ \\ v_y= v_{0} \cdot \sin \alpha - gt \end{cases} $$

Di queste considero solo la componente y

$$ v_y= v_{0} \cdot \sin \alpha - gt $$

Sapendo che l'altezza massima si registra quando la componente y della velocità (v_y=0)

$$ v_{0} \cdot \sin \alpha - gt = 0 $$

Da questa ricavo il tempo di volo (t) necessario per arrivare all'altezza massima (h_max) del lancio.

$$ v_{0} \cdot \sin \alpha = gt $$

$$ t = \frac{ v_{0} \cdot \sin \alpha }{g} $$

Sostituisco t nell'equazione del moto che determina la posizione dell'oggetto sull'asse y

$$ y = y_0 + v_{0} \cdot \sin( \alpha ) \cdot t - \frac{1}{2} g \cdot t^2 $$

$$ y = y_0 + v_{0} \cdot \sin( \alpha ) \cdot [ \frac{ v_{0} \cdot \sin \alpha }{g} ] - \frac{1}{2} g \cdot [ \frac{ v_{0} \cdot \sin \alpha }{g} ]^2 $$

$$ \require{cancel} y = y_0 + \frac{ v^2_{0} \cdot \sin^2 \alpha }{g} - \frac{1}{2} \cancel{g} \cdot \frac{ v^2_{0} \cdot \sin^2 \alpha }{g^{\cancel{2}}} $$

$$ \require{cancel} y = y_0 + \frac{ v^2_{0} \cdot \sin^2 \alpha }{g} - \frac{1}{2} \cdot \frac{ v^2_{0} \cdot \sin^2 \alpha }{g} $$

Se A=v²₀·sin(α)/g allora A-1/2A = 1/2A, ossia una mela meno mezza mela è uguale a mezza mela.

$$ y = y_0 + \frac{1}{2} \cdot \frac{ v^2_{0} \cdot \sin^2 \alpha }{g} $$

Se l'altezza iniziale è y₀=0

$$ y = \frac{1}{2} \cdot \frac{ v^2_{0} \cdot \sin^2 \alpha }{g} $$

E con questo ho dimostrato la formula per determinare l'altezza massima del lancio.

La gittata

La formula per trovare la gittata (G) del lancio del grave è $$ x = \frac{v_0^2 \cdot \sin (2\alpha)}{g} $$

Dimostrazione

Per trovare la gittata devo trovare il tempo di volo necessario perché l'oggetto tocchi terra ossia y=0.

$$ y = 0 $$

Considero la legge del moto sull'asse verticale (y) rispetto al tempo e la eguaglio a zero.

$$ y_0 + v_{0} \cdot \sin( \alpha ) \cdot t - \frac{1}{2} g = 0 $$

Nota. Bisogna però fare attenzione perché ci sono due momenti specifici in cui y=0: quando lancio l'oggetto e quando l'oggetto cade al suolo.

In questo esempio presumo per semplicità che la posizione iniziale sia nulla y₀=0 e coincida con quella di caduta.

In pratica, non ci sono dislivelli di altezza tra il punto di lancio e quello di caduta.

$$ v_{0} \cdot \sin( \alpha ) \cdot t - \frac{1}{2} g \cdot t^2 = 0 $$

Utilizzo quest'ultima equazione per ricavare il tempo di volo (t) necessario perché l'oggetto tocchi terra.

$$ t \cdot ( v_{0} \cdot \sin( \alpha ) - \frac{1}{2} g \cdot t ) = 0 $$

Per la legge di annullamento del prodotto, l'equazione ha due soluzioni

$$ \begin{cases} t = 0 \\ \\ v_{0} \cdot \sin( \alpha ) - \frac{1}{2} g \cdot t = 0 \end{cases} $$

La prima soluzione dell'equazione è la soluzione banale t=0.

Questa soluzione però devo scartarla perché è l'istante in cui sto lanciando l'oggetto.

L'altra soluzione (t>0) è quella, invece, in cui l'oggetto cade al suolo dopo il volo.

$$ v_{0} \cdot \sin( \alpha ) - \frac{1}{2} g \cdot t = 0 $$

Questa soluzione mi permette di ricavare il tempo di volo dal lancio all'impatto al suolo.

$$ v_{0} \cdot \sin( \alpha ) = \frac{1}{2} g \cdot t $$

$$ t = \frac{2 \cdot v_{0} \cdot \sin( \alpha ) }{g} $$

Da notare che il tempo di volo complessivo è esattamente il doppio rispetto al tempo necessario per raggiungere la massima altezza.

Una volta trovato il tempo di volo (t), lo sostituisco nella componente x della legge del moto

$$ x = x_0 + v_0 \cdot \cos( \alpha ) \cdot t $$

Per semplicità considero la posizione iniziale x₀=0.

$$ x = v_0 \cdot \cos( \alpha ) \cdot t $$

Sapendo che il tempo di volo è t=2v₀sin(α)/g

$$ x = v_0 \cdot \cos( \alpha ) \cdot [ \frac{2 \cdot v_{0} \cdot \sin( \alpha ) }{g} ] $$

$$ x = \frac{2 \cdot v^2_{0} \cdot \sin( \alpha ) \cdot \cos( \alpha ) }{g} $$

$$ x = \frac{v^2_{0} \cdot [ 2 \cdot \sin( \alpha ) \cdot \cos( \alpha ) ] }{g} $$

A questo punto applico la formula trigonometrica di duplicazione del seno ossia 2sin(α)cos(α)= sin(2α)

$$ x = \frac{v^2_{0} \cdot \sin( 2 \alpha ) }{g} $$

In questo modo ho dimostrato anche la formula della gittata.

Qual è la massima gittatata possibile? La massima gittata del lancio la ottengo con un angolo di 45°. $$ \alpha = 45° $$ Questo è molto semplice da dimostrare. La funzione trigonometrica del seno assume il suo valore massimo (1) quando l'angolo è uguale a 90°. In questo caso l'argomento del seno è 2α. Quindi, il seno di 2α raggiunge il massimo quando $$ 2 \alpha = 90° $$ ossia $$ \alpha = \frac{90°}{2} = 45° $$ Quest'ultima è l'angolazione ottimale per lanciare l'oggetto il più lontano possibile a parità di velocità iniziale (v₀).

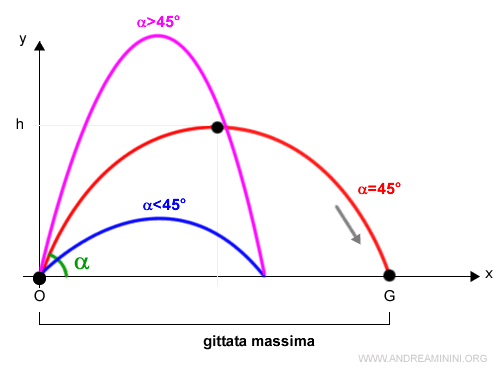
E così via.