Il teorema della traslazione nel tempo
Secondo il teorema della traslazione nel tempo (o teorema del ritardo) della trasformata di Laplace.
La trasformata di Laplace di una funzione f(t) nulla per t<0 ritardata di una durata t0 è: $$ L[f(t-t_0)] = F(s) \cdot e^{-t_0 s} $$
L'entità t0 è detta ritardo finito di lunghezza t0.
L'antitrasformata della funzione traslata è $$ L^{-1}[F(s) \cdot e^{-t_0s} ] = L^{-1}[F(s)] \cdot e^{-(t-t_0)} $$
Esempio
Ho una funzione a gradino
$$ f(t)=A \cdot u(t) = \begin{cases} 0 \:\: \text{per t<0} \\ 1 \:\: \text{per t≥0} \end{cases} $$
Il grafico della funzione è

La trasformata di Laplace è molto semplice.
E' il prodotto di una costante A per una funzione f(t).
$$ L[A \cdot u(t)] $$
Sposto la costante fuori dalla trasformata
$$ A \cdot L[u(t)] $$
Sapendo che la trasformata di un gradino unitario è 1/s, la trasformata di Laplace della funzione è
$$ L[A \cdot u(t)] = A \cdot \frac{1}{s} = \frac{A}{s} $$
Ora traslo la funzione f(t) per un intervallo t0
$$ f(t)=A \cdot u(t-t_0) = \begin{cases} 0 \:\: per \:\: t<t_0 \\ 1 \:\: per \:\: t \ge t_0 \end{cases} $$
Il grafico della funzione è
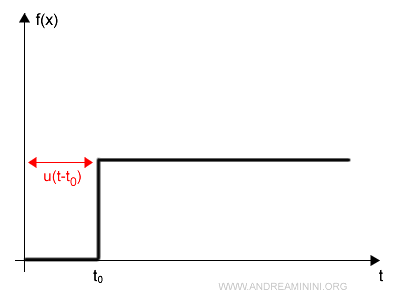
In questo caso applico il teorema della traslazione
$$ L[u(t-t_0)] = \frac{1}{s} e^{-t_0s} $$
Ho così ottenuto la trasformata della funzione traslata.
E così via.
