Teorema della trasformata del prodotto integrale
Date due trasformate di Laplace F1(s) e F2(s) delle funzioni f1(t) e f2(t) vale la seguente relazione $$ L[ \int_0^∞ f_1(τ)f_2(t-τ)dτ] = F_1(s)F_2(s) $$
Dove l'integrale è detto prodotto integrale o integrale di convoluzione delle funzioni f1 e f2.
Per la proprietà commutativa vale l'uguaglianza
$$ \int_0^∞ f_1(τ)f_2(t-τ)dτ = \int_0^∞ f_2(τ)f_1(t-τ)dτ $$
Pertanto posso riscrivere la relazione nel seguente modo:
$$ L[ \int_0^∞ f_1(τ)f_2(t-τ)dτ] = F_1(s)F_2(s) $$ $$ L[ \int_0^∞ f_2(τ)f_1(t-τ)dτ] = F_1(s)F_2(s) $$
Dato un sistema inizialmente in quiete.
$$ Y(s)=G(s)X(s) $$
La funzione G(s) è la funzione di trasferimento del sistema.

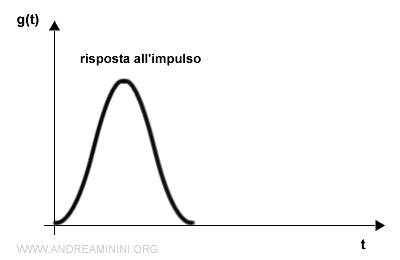
Se la risposta all'impulso X(s) è
$$ g(t) = L^{-1}[G(s)] $$
allora la risposta forzata del sistema è uguale all'antitrasformata della funzione di trasferimento G(s).
Nota. L'antitrasformata della risposta a impulso è L-1[X(s)]=1.
Se la risposa al gradino X(s) è
$$ g_u(t) = L^{-1}[\frac{G(s)}{s}] $$
allora la risposta forzata del sistema è uguale all'antitrasformata della funzione di trasferimento G(s) divisa s.
Nota. L'antitrasformata della risposta a gradino è L-1[X(s)]=1/s.

Quindi, secondo il teorema la risposta forzata del sistema è data da
$$ y(t) = \int_0^∞ x(τ)g(t-τ)dτ $$
$$ y(t) = \int_0^∞ g(τ)x(t-τ)dτ $$
Sono detti integrali di convoluzione o integrali di Duhamel.
Nota. Se l'intervallo è definito si può anche scrivere $$ y(t) \int_0^t f_1(τ)f_2(t-τ)dτ $$
A cosa servono gli integrali di convoluzione?
Gli integrali di convoluzione determinano la risposta forzata del sistema a un qualunque segnale di ingresso x(t) in funzione della risposta all'impulso.
La dimostrazione
La trasformata fondamentale di Laplace è
$$ G(s) = \int_0^{\infty} g(t) \cdot e^{-st} \: dt $$
Dove g(t) è
$$ g(t) = \int_0^t f_1(t-τ)f_2(τ) \: dτ $$
Sostituisco g(t) nella trasformata di Laplace.
$$ G(s) = \int_0^{\infty} g(t) \cdot e^{-st} \: dt $$
$$ G(s) = \int_0^{\infty} [ \int_0^{\infty} f_1(t-τ)f_2(τ) \: dτ ] \cdot e^{-st} \: dt $$
Posso invertire gli integrali tra loro.
Ora dτ è l'integrale esterno mentre dt è quello interno.
$$ G(s) = \int_0^{\infty} [ \int_0^{\infty} f_1(t-τ)f_2(τ) \cdot e^{-st} \: dt ] \: dτ $$
Sposto la funzione f2(τ) fuori dall'integrale interno essendo slegata dalla variabile di derivazione dt.
$$ G(s) = \int_0^{\infty} f_2(τ) \cdot [ \int_0^{\infty} f_1(t-τ) \cdot e^{-st} \: dt ] \: dτ $$
L'integrale interno è la trasformata di Laplace di una funzione traslata.
Nota. La trasformata di Laplace di una funzione traslata è $$ L[ f(t-τ)] = \int_0^{\infty} f(t-τ) \cdot e^{-st} \: dt = F(s) \cdot e^{-st} $$
Quindi, sostituisco l'integrale interno con F1(s)e-st
$$ G(s) = \int_0^{\infty} f_2(τ) \cdot F_1(s) \cdot e^{-st} \: dτ $$
Sposto la funzione F1(s) fuori dall'integrale essendo slegata dalla variabile di derivazione dt.
$$ G(s) = F_1(s) \cdot \int_0^{\infty} f_2(τ) \cdot e^{-st} \: dτ $$
L'ultimo integrale è la trasformata di Laplace della funzione F2(s)
$$ G(s) = F_1(s) \cdot F_2(s) $$
Ho così dimostrato il teorema della convoluzione della trasformata Laplace.
L'interpretazione geometrica
Suddivido l'intervallo di integrazione in n intervalli elementari.
$$ y(t) = \int_0^∞ x(τ)g(t-τ)dτ $$
Poi considero costante il segnale di ingresso x(t) in ogni singolo intervallo.
Il segnale di ingresso si trasforma in una successione di impulsi di intervallo finito.
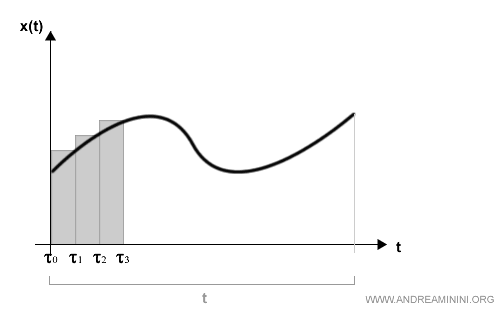
La risposta del sistema approssima l'impulso di Dirac.
$$ x(τ_i) \: Δτ \: g(t-τ_i) $$
La somma delle risposte di tutti gli impulsi approssima la risposta del sistema nel tempo.
$$ y(t) ≅ \sum_{i=1}^{n} x(τ_i) \: Δτ \: g(t-τ_i) $$
Ripeto la stessa procedura anche sull'altro integrale di convoluzione e lo suddivido l'intervallo di integrazione in n intervalli.
$$ y(t) = \int_0^∞ g(τ)x(t-τ)dτ $$
La risposta del sistema è espressa da
$$ x(t-τ_i) \: Δτ \: g(τ_i) $$
La somma delle risposte del sistema in ogni intervallo approssima la risposta complessiva del sistema.
$$ y(t) ≅ \sum_{i=1}^{n} x(t-τ_i) \: Δτ \: g(τ_i) $$
A cosa serve?
Dalla conoscenza della risposta del sistema all'impulso o al gradino, posso risalire alla risposta a qualsiasi segnale di ingresso.
Le formule di Vaschy
Con i teoremi del prodotto integrale e della derivata ottengo le seguenti formule di Vaschy.
$$ y(t) = \int_0^t x'(τ)g_u(t-τ)dτ + x(0)g_u(t) $$
$$ y(t) = \int_0^t g_u(τ)x'(t-τ)dτ + x(0)g_u(t) $$
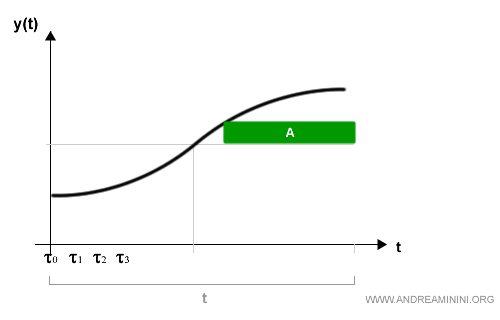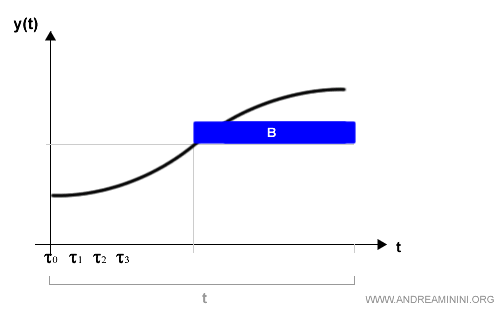
Queste formule approssimano l'incremento della funzione nell'intervallo considerato.
La prima formula approssima l'area A, la seconda l'area B.
E così via.
