La convoluzione
In matematica si dice convoluzione l'integrale del prodotto di una prima funzione f(x) per una seconda funzione g(t) rovesciata e traslata di un certo valore. $$ f(t)*g(t) = \int_{- \infty}^{+ \infty} f(τ)g(t-τ) \: dτ $$ $$ f(t)*g(t) = \int_{- \infty}^{+ \infty} f(t-τ)g(τ) \: dτ $$ E' anche detto integrale di convoluzione.
L'integrale di convoluzione è usato nella teoria dei sistemi.
Un esempio pratico
Ho una funzione x(t) e h(t)
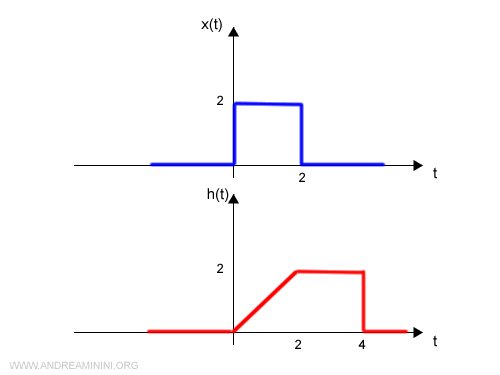
Per ipotesi la funzione x(t) è l'ingresso di un sistema mentre la h(t) è la funzione di trasferimento o di risposta impulsiva del sistema.
Creo una variabile di comodo T=t e la associo alla funzione h(T).
Poi rovescio la funzione in h(-T).
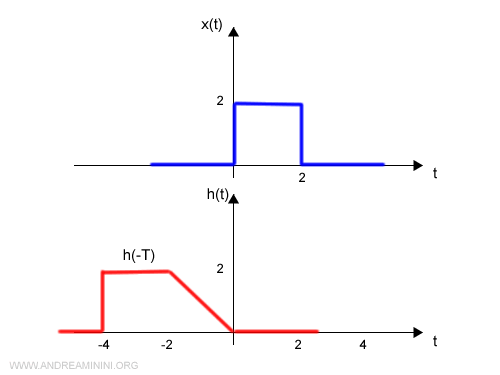
Poi traslo di t la funzione h(t-T)
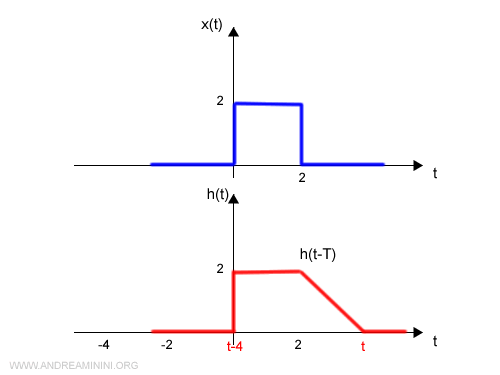
A questo punto calcolo l'integrale del prodotto delle due funzioni x(T)h(t-T) per
$$ x(t)*h(t) = \int_{- \infty}^{+ \infty} x(T)h(t-T) \: dT $$
Nota. L'integrale è calcolato rispetto alla variabile di integrazione T (non t) da -∞ a +∞.
L'integrale determina la convoluzione ossia la funzione y(t)
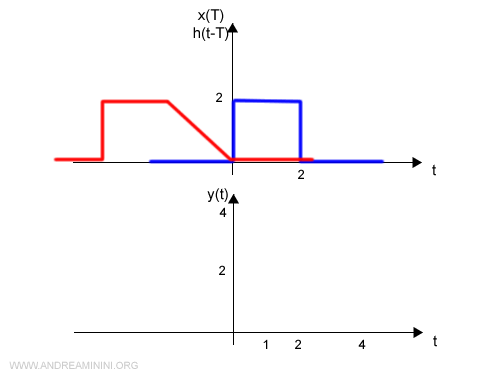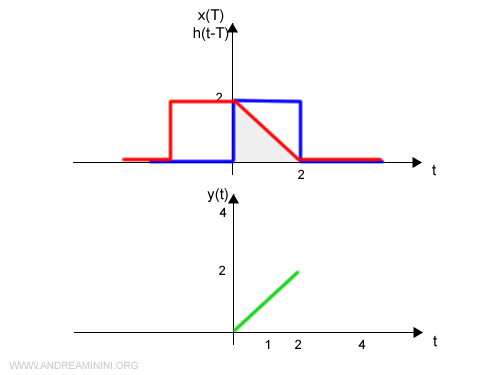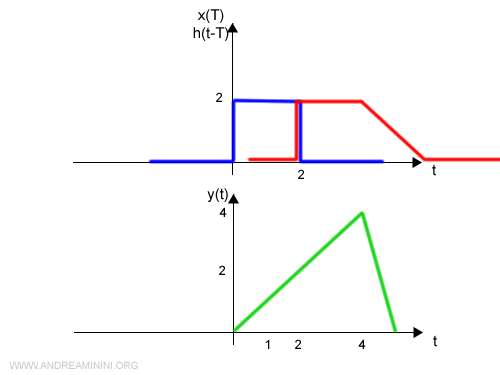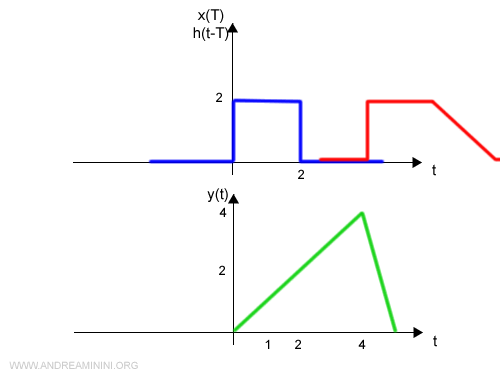
E così via.
