Come cambiare le basi nelle applicazioni lineari

Un'applicazione lineare dipende dagli spazi vettoriali di partenza V (dominio) e di arrivo W (codominio) e dalle basi vettoriali Bv e Bw scelte per i due spazi vettoriali.

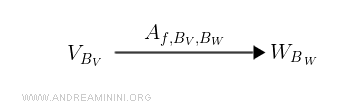
Questa relazione è sintetizzata nella matrice rappresentativa associata all'applicazione lineare.

$$ A_{f,B_V,B_W} $$

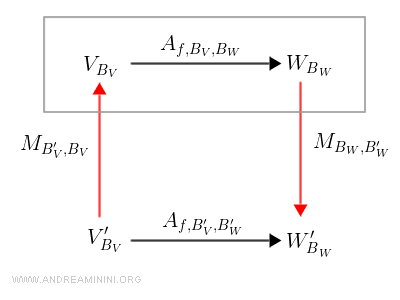
Se decido di cambiare le basi vettoriali, posso apportare le modifiche alla matrice rappresentative tramite la seguente formula.

$$ A_{f,B'_V,B'_W} = M_{B_W,B'_W} A_{f,B_V,B_W} M_{B'_V,B_V} $$

Questa formula usa il legame tra le matrici del cambio di base M dei singoli spazi vettoriali e la matrice rappresentativa A dell'applicazione lineare.

Un esempio pratico di calcolo

Ho due spazi vettoriali V e W nel campo K=R.

$$ V=R^3 \\ W = R^2 $$

L'applicazione lineare è la seguente:

$$ \begin{cases} x-y+z \\ 3x-2y-z \end{cases} $$

Le basi vettoriali di V e W sono le seguenti:

$$ B_V = \begin{pmatrix} 1 & 1 & 2 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix} $$

$$ B_W = \begin{pmatrix} 1 & 2 \\ 1 & 1 \end{pmatrix} $$

Calcolo la matrice rappresentativa A_f associata all'applicazione lineare.

$$ A_{f,B_V,B_W} = \begin{pmatrix} 2 & 2 & 7 \\ -1 & 0 & -3 \end{pmatrix} $$

Come costruire la matrice rappresentativa.
1] Prendo la prima colonna della matrice B_v (1,1,0) e la assegno alle variabili (x,y,z) del sistema per calcolare l'immagine. $$ \begin{pmatrix} x-y+z \\ 3z-2y-z \end{pmatrix} = \begin{pmatrix} 1-1+0 \\ 3(1)-2(1)-1(0) \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$ Calcolo le coordinate dell'immagine rispetto alla base Bw. $$ \begin{pmatrix} 0 \\ 1 \end{pmatrix} = a_1 \begin{pmatrix} 1 \\ 1 \end{pmatrix} + a_2 \begin{pmatrix} 2 \\ 1 \end{pmatrix} $$ La soluzione dell'equazione vettoriale è a₁=2 e a₂=-1 ho così ottenuto la prima colonna della matrice rappresentativa. $$ A_{f,B_V,B_W} = \begin{pmatrix} 2 & ? & ? \\ -1 & ? & ? \end{pmatrix} $$ 2] Prendo la seconda colonna della matrice B_v (1,0,1) e la assegno alle variabili (x,y,z) del sistema per calcolare l'immagine. $$ \begin{pmatrix} x-y+z \\ 3z-2y-z \end{pmatrix} = \begin{pmatrix} 1-0+1 \\ 3(1)-2(0)-1(1) \end{pmatrix} = \begin{pmatrix} 2 \\ 2 \end{pmatrix} $$ Calcolo le coordinate dell'immagine rispetto alla base Bw. $$ \begin{pmatrix} 2 \\ 2 \end{pmatrix} = a_1 \begin{pmatrix} 1 \\ 1 \end{pmatrix} + a_2 \begin{pmatrix} 2 \\ 1 \end{pmatrix} $$ La soluzione dell'equazione vettoriale è a₁=2 e a₂=0 ho così ottenuto la seconda colonna della matrice rappresentativa. $$ A_{f,B_V,B_W} = \begin{pmatrix} 2 & 2 & ? \\ -1 & 0 & ? \end{pmatrix} $$ 3] Prendo la terza colonna della matrice B_v (2,1,0) e l'assegno alle variabili (x,y,z) del sistema per calcolare l'immagine. $$ \begin{pmatrix} x-y+z \\ 3z-2y-z \end{pmatrix} = \begin{pmatrix} 2-1+0 \\ 3(2)-2(1)-1(0) \end{pmatrix} = \begin{pmatrix} 1 \\ 4 \end{pmatrix} $$ Calcolo le coordinate dell'immagine rispetto alla base Bw. $$ \begin{pmatrix} 1 \\ 4 \end{pmatrix} = a_1 \begin{pmatrix} 1 \\ 1 \end{pmatrix} + a_2 \begin{pmatrix} 2 \\ 1 \end{pmatrix} $$ La soluzione dell'equazione vettoriale è a₁=7 e a₂=-3 ho così ottenuto la seconda colonna della matrice rappresentativa. $$ A_{f,B_V,B_W} = \begin{pmatrix} 2 & 2 & 7 \\ -1 & 0 & -3 \end{pmatrix} $$

Il cambio di base

Cambio le basi degli spazi vettoriali V e W con le seguenti

$$ B'_V = \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 2 & 1 & 0 \end{pmatrix} $$

$$ B'_W = \begin{pmatrix} 1 & 1 \\ 1 & 3 \end{pmatrix} $$

Quindi calcolo le matrici del cambio di base

$$ M_{B_V,B'_V} = \begin{pmatrix} 2 & 3 & - 2 \\ 1 & 0 & 0 \\ 0 & 2 & -1 \end{pmatrix} $$

$$ M_{B_W,B'_W} = \begin{pmatrix} 1 & 5/2 \\ 0 & -1/2 \end{pmatrix} $$

Come calcolare le matrici del cambio di base $$ M_{B_V,B'_V} = B_V \cdot [B'_V]^{-1} = \begin{pmatrix} 1 & 1 & 2 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 2 & 1 & 0 \end{pmatrix} ^{-1} = \begin{pmatrix} 2 & 3 & - 2 \\ 1 & 0 & 0 \\ 0 & 2 & -1 \end{pmatrix} $$ $$ M_{B_W,B'_W} = B_W \cdot [B'_W]^{-1} = \begin{pmatrix} 1 & 2 \\ 1 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 1 \\ 1 & 3 \end{pmatrix} ^{-1} = \begin{pmatrix} 1 & 5/2 \\ 0 & -1/2 \end{pmatrix} $$

Ho quasi tutti gli elementi del cambio di base.

$$ A_{f,B'_V,B'_W} = M_{B_W,B'_W} \cdot A_{f,B_V,B_W} \cdot M_{B'_V,B_V} $$

Manca soltanto l'ultimo fattore M_B'v,Bv

$$ A_{f,B'_V,B'_W} = \begin{pmatrix} 1 & 5/2 \\ 0 & -1/2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 & 7 \\ -1 & 0 & -3 \end{pmatrix} \cdot M_{B'_V,B_V} $$

Posso ottenerlo calcolando la matrice inversa della matrice M_BV,B'V che già conosco

$$ M_{B_V,B'_V}^{-1} = \begin{pmatrix} 2 & 3 & - 2 \\ 1 & 0 & 0 \\ 0 & 2 & -1 \end{pmatrix} ^{-1} = \begin{pmatrix} 0 & 1 & 0 \\ -1 & 2 & 2 \\ -2 & 4 & 3 \end{pmatrix} = M_{B'_V,B_V} $$

Quindi

$$ M_{B'_V,B_V} = \begin{pmatrix} 0 & 1 & 0 \\ -1 & 2 & 2 \\ -2 & 4 & 3 \end{pmatrix} $$

A questo punto ho tutti gli elementi per calcolare il cambio di base dell'applicazione.

$$ A_{f,B'_V,B'_W} = M_{B_W,B'_W} \cdot A_{f,B_V,B_W} \cdot M_{B'_V,B_V} $$

$$ A_{f,B'_V,B'_W} = \begin{pmatrix} 1 & 5/2 \\ 0 & -1/2 \end{pmatrix} \begin{pmatrix} 2 & 2 & 7 \\ -1 & 0 & -3 \end{pmatrix} \begin{pmatrix} 0 & 1 & 0 \\ -1 & 2 & 2 \\ -2 & 4 & 3 \end{pmatrix} $$

$$ A_{f,B'_V,B'_W} = \begin{pmatrix} -5 & 10.5 & 8 \\ -16 & 34 & 25 \end{pmatrix} $$

Ho così trovato la matrice associata dell'applicazione lineare dopo il cambio di base.