Teorema della radice della serie numerica
Data una successione a termini non negativi an, se esiste il limite della radice $$ l = \lim_{n \rightarrow \infty} \sqrt[n]{a_n} $$ la serie è convergente se l<1 $$ l<1 \Rightarrow \sum_{k=1}^{\infty} a_k < + \infty $$ la serie è divergente se l>1 $$ l>1 \Rightarrow \sum_{k=1}^{\infty} a_k = + \infty $$
E' uno dei criteri di convergenza (o divergenza) delle serie numeriche.
Se il limite è uguale a uno, il teorema della radice non è applicabile per stabilire il carattere della serie.
Nota. Se il limite è uguale a uno devo usare un altro criterio di convergenza.
Un esempio pratico
Esempio 1
Devo studiare il carattere della serie
$$ \sum_{n=1}^{\infty} \frac{1}{2^n } $$
E' una serie a termini non negativi, quindi posso usare il criterio della radice.
Calcolo il limite della radice della successione.
$$ \lim_{n \rightarrow \infty } \sqrt[n]{ \frac{1}{2^n } } $$
$$ \lim_{n \rightarrow \infty } \frac{\sqrt[n]{1}}{\sqrt[n]{2^n} } $$
$$ \lim_{n \rightarrow \infty } \frac{1}{2} = \frac{1}{2} < 1$$
Il limite è minore di 1.
Pertanto, secondo il criterio della radice la serie Σ 1/2n è una serie convergente.
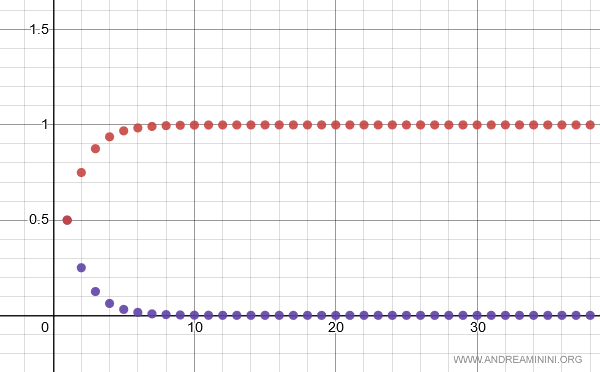
Ovviamente, la serie è convergente ma non è detto che converga a 1/2.
Verifica. Ecco l'andamento della serie Σ 1/2n , la serie converge asintoticamente a 1.
Esempio 2
Devo studiare il carattere della seguente serie:
$$ \sum_{n=1}^{\infty} \frac{1}{ ( \log n )^{\frac{n}{2} } } $$
Per farlo applico il teorema della radice.
Calcolo il limite della radice della successione.
$$ \lim_{n \rightarrow \infty} \sqrt[n]{ \frac{1}{ ( \log n )^{\frac{n}{2} } } } $$
ossia
$$ \lim_{n \rightarrow \infty} [ \frac{1}{ ( \log n )^{\frac{n}{2} } } ]^{\frac{1}{n}} $$
Dopo la semplificazione algebrica diventa
$$ \lim_{n \rightarrow \infty} \frac{1}{ ( \log n )^{\frac{1}{2} } } $$
$$ \lim_{n \rightarrow \infty} ( \log n )^{ - \frac{1}{2} } $$
Il limite tende a zero per n→∞
$$ \lim_{n \rightarrow \infty} ( \log n )^{ - \frac{1}{2} } = 0 < 1 $$
Quindi, secondo il teorema della radice la serie è una serie convergente perché il limite è minore di 1
$$ \sum_{n=1}^{\infty} \frac{1}{ ( \log n )^{\frac{n}{2} } } = \: convergente $$
Ecco la rappresentazione grafica della serie
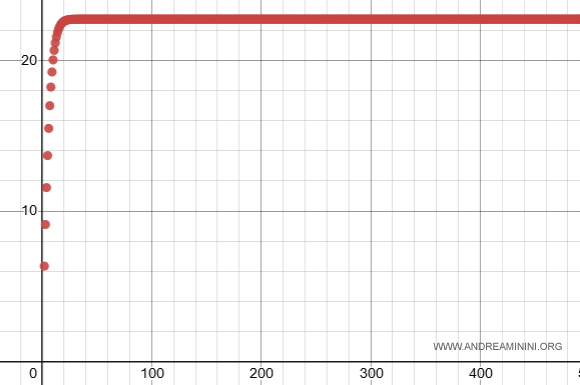
Effettivamente è una serie convergente.
La dimostrazione
1] Serie convergente
Se il limite è inferiore a 1.
$$ l = \lim_{n \rightarrow \infty} \sqrt[n]{a_n} < 1 $$
Preso un valore ε>0 tale che
$$ l+ε < 1 $$
Per la definizione delle successioni convergenti esiste un indice v tale che per ogni n>v
$$ \sqrt[n]{a_n}< l+ε $$
ossia
$$ a_n< (l+ε)^n $$
Ottengo così due successioni confrontabili.
Applico la sommatoria a entrambi i membri per ottenere le rispettive serie delle due successioni
$$ \sum_{n=1}^{\infty} a_n < \sum_{n=1}^{\infty} (l+ε)^n $$
Al secondo membro della disequazione c'è la serie geometrica.
La serie geometrica è una serie convergente se la ragione è minore di 1. Come in questo caso, poiché l+ε<1.
Se la serie a destra converge a l', per il teorema del confronto delle serie anche la serie a sinistra è una serie convergente.
$$ \sum_{n=1}^{\infty} a_n < l' $$
Ho così dimostrato la convergenza della serie.
2] Serie divergente
Se il limite è maggiore di 1.
$$ l = \lim_{n \rightarrow \infty} \sqrt[n]{a_n} > 1 $$
Esiste un indice v tale che per ogni n>v
$$ \forall n>v \in N \: : \: \sqrt[n]{a_n} > 1 $$
ossia
$$ \forall n>v \in N \: : \: (\sqrt[n]{a_n})^n > (1)^n $$
$$ \forall n>v \in N \: : \: a_n > 1 $$
Pertanto, il limite della successione an non tende a zero.
$$ \lim_{n \rightarrow \infty} a_n \ne 0 $$
Viene meno la condizione necessaria per la convergenza della serie.
Se la serie non è convergente, allora la serie è divergente.
Nota. Per l'ipotesi iniziale la successione an è a termini positivi. Quindi anche la serie è a termini non negativi che ammette sempre un limite finito o infinito. Quindi, la serie converge o diverge. Non può essere indeterminata. Per cui se non converge, allora diverge.
E così via.
