Monomi

Un monomio è un'espressione letterale composta da un solo termine in cui compaiono sono moltiplicazioni e potenze in cui gli esponenti delle variabili sono numeri naturali.

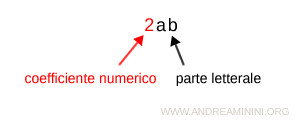
Il fattore numerico è detto coefficiente del monomio mentre le lettere sono dette parte letterale del monomio.

I coefficienti numerici possono anche avere esponenti negativi ( es. $4^{-1} = \frac{1}{4}$ ) mentre quelli delle variabili sono esclusivamente numeri naturali ( es. $x^0, x^1, x^2, ...$ ).

Esempi di monomi

Per capire meglio cosa è un monomio e cosa non lo è, prendo in considerazione alcuni esempi pratici.

Ecco un esempio di monomio:

$$2a^3b^4$$

Il coefficiente del monomio è 2 mentre la parte letterale è a³b⁴

Nota. In un monomio gli esponenti delle lettere sono esclusivamente dei numeri naturali. Inoltre, se il coefficiente numerico è 1 o -1 non si scrive perché è sottinteso. Ad esempio si scrive a, -a. $$a \ , \ -a$$ Non si scrive 1a o -1a.

Viceversa, questo non è monomio perché è composto da due termini

$$2a^3 + b^4$$

E' una somma algebrica di monomi. In questo caso si parla più propriamente di polinomio.

Nota. Si chiama monomio perché significa "un solo termine". Nell'espressione 2a³+b⁴ ce ne sono due. La parola "monomio" è l'unione della parola greca monos (unico) con la parola latina nomen (nome o termine).

Anche questo non è un monomio perché una variabile compare al denominatore, ossia ha una potenza con esponente negativo.

$$2a^3b^{-4} = \frac{2a^3}{b^4}$$

Questo invece è un monomio perché i coefficienti numerici possono avere un esponente negativo.

$$2^{-3}a^3b^4 = \frac{a^3b^4}{2^3}$$

Sono monomi anche le singole lettere (ad esempio a, b, c, ecc. ) e i singoli numeri (es. 1, 2, 3, ecc. )

Ad esempio, un numero reale è un monomio perché può essere visto come il prodotto tra il numero e una variabile con esponente zero.

$$3 = 3 \cdot a^0 = 3 \cdot 1$$

Nota. Questo significa che l'insieme dei numeri reali $\mathbb{R}$ è un sottoinsieme dell'insieme dei monomi.

Anche il numero zero è un monomio. Quando il coefficiente numerico è zero si parla di monomio nullo.

$$0 = 0 \cdot a^0 = 0 \cdot 1$$

Infine, le singole lettere sono monomi perché sono il prodotto tra il numero 1 e la lettera stessa.

$$a = 1 \cdot a$$

Questi esempi dovrebbero fugare ogni dubbio su cosa sono i monomi.

La forma normale del monomio

Un monomio è detto monomio ridotto alla forma normale quando è scritto come il prodotto di un unico coefficiente numerico e di potenze di lettere, ciascuna con base diversa dalle altre.

Esempio

Questo monomio non è in forma normale perché la lettera "a" compare due volte e ci sono anche due coefficienti numerici.

$$2a^23b^3a$$

Per trasformarlo in forma normale raggruppo i coefficienti numerici e le lettere uguali usando la proprietà commutativa e associativa della moltiplicazione

$$(2 \cdot 3) \cdot (a^2 \cdot a) \cdot b^3$$

Calcolo il prodotto dei numeri

$$6 (a^2 \cdot a) \cdot b^3$$

Poi calcolo il prodotto tra le lettere uguali usando la proprietà delle potenze

$$6 (a^{2+1}) \cdot b^3$$

In questo modo ottengo il monomio in forma normale.

$$6 a^3b^3$$

Il grado di un monomio

Il grado di un monomio è uguale alla somma degli esponenti di tutte le lettere che compongono il monomio

Nel computo non vanno considerati i coefficienti numerici.

Il monomio è detto di grado zero quando non ci sono lettere nel monomio.

Nota. Nel caso particolare del monomio nullo (es. 0), ossia dello zero, non si attribuisce nessun grado al monomio. Questo perché può essere ottenuto in diversi modi, quindi è indeterminato. Ad esempio, $0 = 0 \cdot x^0 = 0 \cdot x^1 = 0 \cdot x^2 =...$

Esempio

Questo monomio è di grado 4 perché l'esponente della lettera "a" è tre e quello della lettera "b" è uno (3+1=4).

$$2 a^3b$$

Esempio 2

Questo monomio è di grado 5 perché l'esponente delle lettera "a" e "b" è due mentre quello della lettera "c" è uno (2+2+1=5).

$$2 a^2b2c$$

Esempio 3

Ogni numero non nullo ha grado zero perché può essere scritto come un prodotto con una variabile di grado 0.

$$1 = 1 \cdot x^0$$

$$2 = 2 \cdot x^0$$

$$3 = 3 \cdot x^0$$

Fa eccezione solo lo zero che ha grado indeterminato.

Grado di un monomio rispetto a una variabile

Il grado di un monomio rispetto a una variabile è definito come l’esponente con cui quella variabile compare nel monomio ridotto in forma normale.

Per stabilire il grado rispetto a una variabile, devo prima ridurre il monomio alla forma normale, poi osservo l’esponente della variabile considerata.

Esempio

Considero questo monomio

$2x \cdot x^2 \cdot y$

Si tratta di un monomio non ridotto perché compaiono potenze con la stessa base più volte.

Quindi, riduco il monomio in forma normale.

$$5x^3y^2$$

Ora posso calcolare il grado delle variabili.

Il grado rispetto a $x$ è 3 mentre il grado rispetto a $y$ è 2

Nota. Se in un’espressione una variabile ha esponente 0 (cioè non è presente), il grado rispetto a quella variabile è 0. Ad esempio, nel monomio $5x^3y^2$ il grado della variabile $z$ è zero, perché la variabile $z$ non è presente nel monomio.

Variabili e costanti nei monomi

In un monomio, le lettere si trattano come variabili per impostazione predefinita.

Tuttavia, ci sono casi particolari in cui una lettera ha un valore fisso (come π) e non è una variabile ma una costante, quindi non fa parte della parte letterale.

La parte letterale è il prodotto di tutte le variabili. Non si includono numeri e nemmeno lettere che rappresentano costanti.

Le costanti, anche se espresse con lettere come π, rientrano nel coefficiente numerico del monomio, perché rappresentano dei valori fissi ossia "non variabili".

Esempio

Nel monomio $\frac{4}{3} \pi r^3$, che rappresenta il volume di una sfera, π è una costante (approssimabile a 3,14), mentre $r$ è la variabile (il raggio della sfera).

In questo caso la parte letterale del monomio è solo $r^3$, perché π non è una variabile.

La costante pi greco (π) fa parte del coefficiente numerico del monomio che in questo caso è $\frac{4}{3} \pi$.

Nota. A volte le costanti sono universalmente riconosciute in matematica o in fisica tramite un simbolo ben noto. Ad esempio, il pi greco (π), il numero di nepero (e), ecc. A volte, il contesto o il testo definisce che una certa lettera rappresenta un valore costante. Quindi, per identificare correttamente la parte letterale, bisogna sempre capire il significato delle lettere usate nel monomio e ricordarsi che solo le variabili ne fanno parte. Ad esempio, nel monomio $7k\alpha^2$, se so che $\alpha$ è una costante fisica allora la parte letterale è solo $k$. Se invece non c’è indicazione, posso assumere che anche $\alpha$ sia una variabile, e quindi la parte letterale è $k\alpha^2$.

E così via.