Le operazioni matematiche tra monomi
Le principali operazioni matematiche tra monomi
L'addizione tra monomi
L'addizione tra due o più monomi con la stessa parte letterale (monomi simili) si ottiene raccogliendo il fattore comune e sommando i coefficienti numerici.

La somma di due monomi è un altro monomio.
L'addizione tra due monomi è possibile solo se hanno la stessa parte laterale, ossia sono monomi simili. In caso contrario non è possibile.
Esempio. Considero la somma di due monomi $$ 2a^3 + 4a^3 $$ raccolgo il fattore comune $$ (2+3) \cdot a^3 $$ Sommo i coefficienti algebrici $$ 5a^3 $$ Il risultato è la somma algebrica dei due monomi.
Esempio 2. Considero la somma di due monomi $$ 2a^3 + 5a^2 $$ In questo caso l'espressione non posso semplificarla perché la parte letterale è diversa e l'addizione non è possibile.
L'addizione non è una operazione interna ai monomi, perché la somma non è detto che sia ancora un monomio.
Ad esempio, se i monomi non sono simili il risultato finale è un polinomio.
Esempio. Questa è un'addizione tra due monomi non simili $$ 3x^2 + 4x $$ In questo caso il risultato è un polinomio. Non è un monomio.
La sottrazione tra monomi
La sottrazione tra due o più monomi con la stessa parte letterale (monomi simili) si ottiene raccogliendo il fattore comune e calcolando la differenza dei coefficienti numerici.

La differenza di due monomi è un altro monomio.
Anche in questo caso la differenza non è possibile se i monomi hanno parti letterali differenti.
Esempio. Devo sottrarre due monomi $$ 2a^3 - 5a^3 $$ raccolgo il fattore comune $$ (2-5) \cdot a^3 $$ Calcolo la differenza dei coefficienti algebrici $$ -3a^3 $$ Il risultato è la differenza algebrica dei monomi.
Esempio 2. In questo caso non posso calcolare la differenza trai due monomi $$ 2a^3 + 5a^2 $$ perché le parti letterali sono diverse e l'espressione non è semplificabile.
La sottrazione tra due monomi simili può anche essere vista come la somma del primo con l'opposto del secondo.
Esempio. Per sottrarre due monomi $$ 2a^3 - 5a^3 $$ sommo il primo monomio $ 2a^3 $ per l'opposto del secondo $ -5a^3 $ che in questo caso è $ 5a^3 $ $$ (2a^3) - (5a^3) = 2a^3 + (- 5a^3) = -3a^3 $$
Merita d'essere sottolineato che la sottrazione non è una operazione interna ai monomi, perché il risultato non è detto che sia sempre un monomio. Se i monomi non sono simili il risultato è un polinomio.
La moltiplicazione tra monomi
Il prodotto tra monomi è un monomio che ha come coefficiente il prodotto dei coefficienti numerici dei monomi e come parte letterale il prodotto delle parti letterali dei monomi.
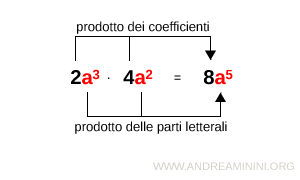
La moltiplicazione tra monomi non richiede che i monomi siano monomi simili, potrebbero anche non esserlo.
Per calcolare il prodotto tra monomi è necessario conoscere le proprietà delle potenze.
Esempio. Devo moltiplicare due monomi $$ 4a^2b \cdot 5a^3c $$ Utilizzo la proprietà associativa e commutativa per raggruppare il prodotto dei coefficienti numerici e il prodotto delle parti letterali $$ (4 \cdot 5) \cdot (a^2b \cdot a^3c) $$ Calcolo il prodotto dei coefficienti $$ 20 \cdot (a^2b \cdot a^3c) $$ Poi calcolo il prodotto delle parti letterali raggruppando le stesse lettere $$ 20 \cdot (a^2 \cdot a^3) \cdot b \cdot c $$ Utilizzo le proprietà delle potenze nei prodotti tra le stesse lettere $$ 20 \cdot (a^{2+3}) \cdot bc $$ Il risultato è il prodotto algebrico dei monomi. $$ 20a^5bc $$
Se uno dei due monomi è lo zero, il risultato è sempre il monomio nullo, perché lo zero è l'elemento assorbente rispetto alla moltiplicazione anche nell'insieme dei monomi.
Esempio. Considero il prodotto tra un monomio e lo zero $$ 4a^2b \cdot 0 = (4 \cdot 0) \cdot a^2b = 0 \cdot a^2b = 0 $$
Il prodotto di due monomi è sempre un monomio, quindi la moltiplicazione è un'operazione interna all'insieme dei monomi.
La divisione tra monomi
La divisione tra monomi è un monomio che ha come coefficiente il quoziente dei coefficienti numerici dei monomi e come parte letterale il quoziente delle parti letterali dei monomi. Il divisore non deve essere nullo.
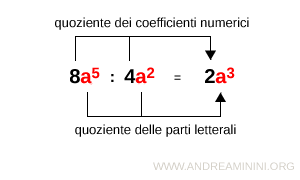
Anche nel caso della divisione non occorre che il monomio dividendo e il monomio divisore siano monomi simili.
E' invece necessario che il monomio divisore non sia nullo perché la divisione per zero è un'operazione impossibile.
Per calcolare il quoziente tra monomi è necessario applicare le proprietà delle potenze.
Esempio. Devo dividere due monomi $$ 8a^4b : 4a^3c $$ Riscrivo la divisione come frazione $$ \frac{8a^4b}{4a^3c} $$ Utilizzo la proprietà associativa e commutativa per raggruppare il quoziente dei coefficienti numerici e il quoziente delle parti letterali $$ \frac{8}{4} \cdot \frac{a^4b}{a^3c} $$ Calcolo il quoziente dei coefficienti numerici $$ 2 \cdot \frac{a^4b}{a^3c} $$ Poi calcolo il quoziente delle parti letterali $$ 2 \cdot a^4b \cdot a^{-3}c^{-1} $$ $$ 2 \cdot a^{4-3}bc^{-1} $$ $$ 2 \cdot abc^{-1} $$ $$ \frac{2ab}{c} $$ Il risultato è il monomio quoziente.
La divisione non è un'operazione interna all'insieme dei monomi perché il risultato può anche essere una frazione algebrica.
Ad esempio, il risultato della divisione $ \frac{2a^2b}{ac} = \frac{2ab}{c} $ non è un monomio ma una frazione algebrica.
La potenza di un monomio
La potenza di un monomio è un monomio che ha per coefficiente numerico la potenza del coefficiente numerico del monomio e per parte letterale la potenza della parte letterale del monomio.

Per calcolare la potenza n-esima di un monomio occorre conoscere le proprietà delle potenze.
Si eleva il coefficiente alla potenza n e si moltiplicano per n gli esponenti di ciascun fattore della parte letterale.
Esempio. Devo calcolare la potenza del monomio $$ (4a^3b)^2 $$ Calcolo la potenza del coefficiente numerico $$ 4^2 \cdot (a^3b)^2 $$ $$ 16 \cdot (a^3b)^2 $$ Calcolo la potenza della parte letterale applicando le proprietà delle potenze. $$ 16 \cdot a^{3 \cdot 2} \cdot b^2 $$ Il risultato è la potenza del monomio. $$ 16a^6b^2 $$
La potenza con esponente 0 di qualsiasi monomio è sempre uguale a 1.
$$ (4a^3b)^0 = 4^0 \cdot a^{3 \cdot 0} b^0 = 1 $$
Poiché la potenza $ 0^0 $ non è definita, non è possibile nemmeno definire la potenza con esponente zero di un monomio nullo.
L'elevamento a potenza è una operazione interna dei monomi, perché il risultato è ancora un monomio.
E così via.
