Piano secante, tangente o esterno a una sfera

Un piano a può essere secante, tangente oppure esterno rispetto a una sfera con centro C e raggio r se la distanza tra il piano e il centro della sfera è rispettivamente inferiore, uguale o maggiore del raggio. $$d(C,a)<r \:\: secante \\ d(C,a)=r \:\: tangente \\ d(C,a)>r \:\: esterno$$

Un esempio pratico

Data una sfera con il centro C alle coordinate (x,y,z) dello spazio e un raggio uguale a due.

$$C = \begin{pmatrix} 5 \\ 3 \\ 2 \end{pmatrix}$$

$$r = 2$$

Prendo un piano α nello spazio

$$α: -3x+2y+z=0$$

Devo verificare se il piano è secante, tangente o esterno alla sfera.

Calcolo la distanza tra il punto centrale C della sfera e il piano.

$$d(C,α) = \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+b^2}}$$

$$d(C,α) = \frac{|-3x_0+2y_0+1z_0+d|}{\sqrt{(-3)^2+2^2+1^2}}$$

$$d(C,α) = \frac{|-3(5)+2(3)+1(2)+0|}{\sqrt{(-3)^2+2^2+1^2}}$$

$$d(C,α) = \frac{|-15+6+2|}{\sqrt{9+4+1}}$$

$$d(C,α) = \frac{|-7|}{\sqrt{14}}$$

$$d(C,α) = \frac{7}{\sqrt{14}} \approx 1.87$$

La distanza tra il piano e il centro della sfera è inferiore al raggio.

$$d(C,α) \approx 1.87 < r = 2$$

Quindi il piano è secante alla sfera.

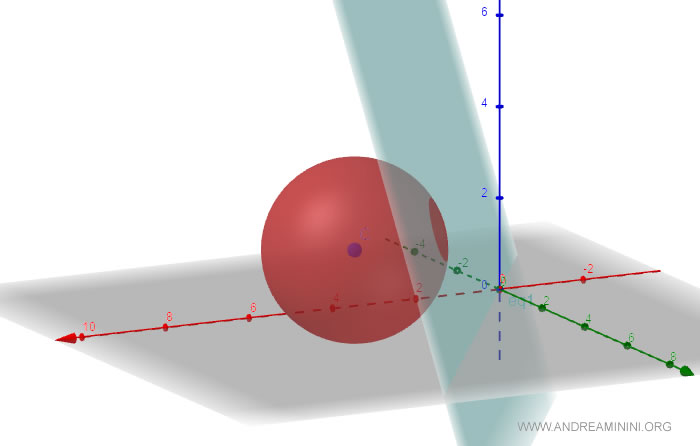
E così via.