Punti interni ed esterni alla sfera
Rispetto alla sfera i punti possono essere
- Punti interni se la distanza del punto P dal centro C della sfera è inferiore al raggio r. $$ d(C,P)<r $$
- Punti esterni se la distanza del punto P dal centro C della sfera è superiore al raggio r. $$ d(C,P)>r $$
Un esempio pratico
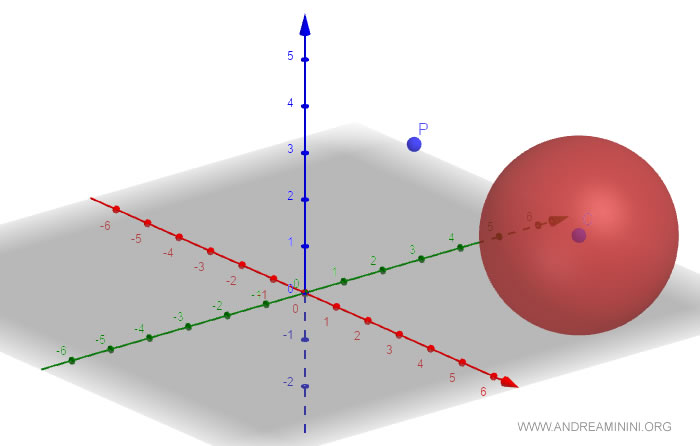
Ho una sfera con il centro alle coordinate (x,y,z) dello spazio e un raggio uguale a due.
$$ C = \begin{pmatrix} 5 \\ 3 \\ 2 \end{pmatrix} $$
$$ r = 2 $$
Prendo un punto P dello spazio alle seguenti coordinate
$$ P = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$
Devo capire se è un punto interno o esterno alla sfera.
Quindi calcolo la distanza tra i due punti CP.
$$ ||\overrightarrow{CP}|| = \sqrt{(5-1)^2+(3-2)^2+(2-3)^2} $$
$$ ||\overrightarrow{CP}|| = \sqrt{(4)^2+(1)^2+(1)^2} $$
$$ ||\overrightarrow{CP}|| = \sqrt{18} \approx 4.24 $$
La distanza tra i due punti è 4.24 ed è maggiore del raggio r=2 della sfera.
$$ d(C,P)=4.24 > r = 2 $$
Quindi il punto P è esterno alla sfera.
E così via.
