Moti curvilinei

Cosa sono i moti curvilinei

I moti curvilinei sono moti che hanno una traiettoria su una linea curva. Può trattarsi di un cerchio o una parabola. Possono essere periodici o meno.

Tipi di moti curvilinei

I principali moti curvilinei sono:

• Il moto circolare uniforme
  La traiettoria è una circonferenza in cui il corpo si sposta con velocità costante (uniforme)
• Il moto circolare vario
  La traiettoria è una circonferenza, in cui il corpo si sposta con velocità variabile.
• Il moto parabolico
  La traiettoria è una parabola. Ad esempio, la caduta dei gravi.

La differenza tra moti curvilinei e rettilinei

I moti curvilinei sono più complessi dei moti rettilinei, perché la velocità e l'accelerazione devono essere studiate anche su distanze angolari oltre che lineari.

E' necessario studiarle come grandezze vettoriali.

La velocità nei moti curvilinei

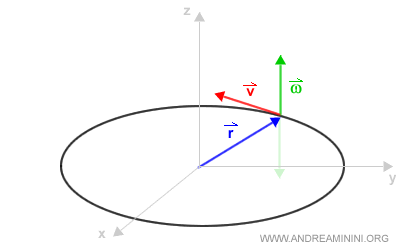
Quando un corpo si muove su una curva, il vettore velocità (v) modifica la direzione durante il moto perché deve essere sempre tangente alla traiettoria. E' il vettore rosso.

Viceversa, in un moto rettilineo la direzione del vettore velocità è sempre la stessa.

Il modulo della velocità |v| può anche cambiare ma la direzione del vettore v è costante.

Inoltre, in un moto curvilineo si possono considerare due tipi di velocità:

• La velocità (v)
  E' la velocità di spostamento del corpo sulla traiettoria.
• La velocità angolare (ω)
  E' la velocità di variazione dell'angolo che congiunge il centro della circonferenza con la posizione del corpo sulla traiettoria. E' perpendicolare al piano. Nell'esempio precedente è il vettore verde.

L'accelerazione nei moti curvilinei

Nei moti curvilinei l'accelerazione è composta da due componenti:

• L'accelerazione tangenziale
  Misura la variazione del modulo della velocità |v| ossia della lunghezza del vettore velocità v. E' tangente alla traiettoria e ha verso uguale al moto del corpo. $$ \frac{|Dv|}{Dt} $$
• L'accelerazione normale o centripeta
  Misura la variazione di direzione del vettore velocità nel corso del tempo. E' perpendicolare alla traiettoria e ha un verso diretto alla concavità della linea curva.

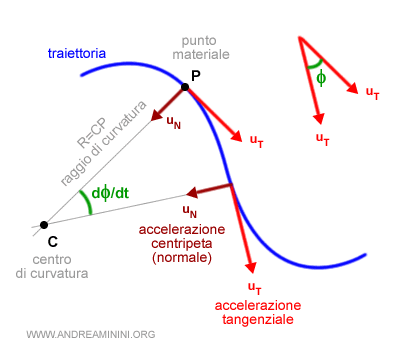
Nota. L'accelerazione normale (a_N) è detta centripeta in un moto circolare perché la direzione del vettore a_N (verde) punta sempre verso il centro della circonferenza. Viceversa, in un moto parabolico la parte concava della curva può variare e cambia anche il verso del vettore a_N (verde).

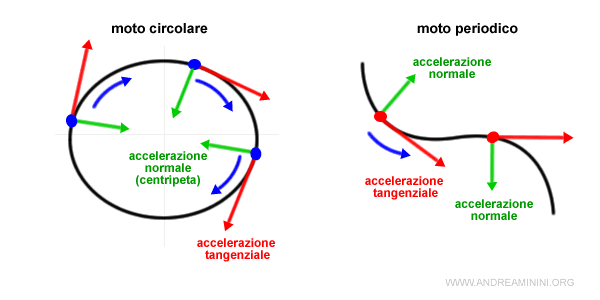
Per un approfondimento sulla natura vettoriale dell'accelerazione ho scritto un appunto sulla differenza tra accelerazione tangenziale e normale.

I moti curvilinei periodici

Alcuni moti curvilinei sono anche moti periodici.

In questi casi devo considerare concetti quali il periodo e la frequenza.

• Il periodo
  Il periodo (T) è il tempo impiegato dal corpo per compiere un giro.
• La frequenza
  La frequenza (f) è il numero di giri compiuti dal corpo in un secondo.

Il periodo e la frequenza sono inversamente relazionati tra loro.

$$ f = \frac{1}{T} $$

$$ T = \frac{1}{f} $$

Nota. Un esempio di moto curvilineo periodico è il moto circolare. Dal moto circolare deriva il moto armonico che, pur essendo un moto rettilineo, è anche un moto periodico. Il moto armonico può essere visto come la proiezione di un moto circolare su un asse cartesiano.

E così via.