La rappresentazione polare dei numeri complessi
I numeri complessi possono essere rappresentati anche in forma polare.
Le coordinate polari di un numero complesso sono la lunghezza r (detta modulo) e l'angolo α del segmento orientato (vettore) che congiunge l'origine O (polo) con le coordinate cartesiane (x,y) del numero complesso z sul piano di Gauss.
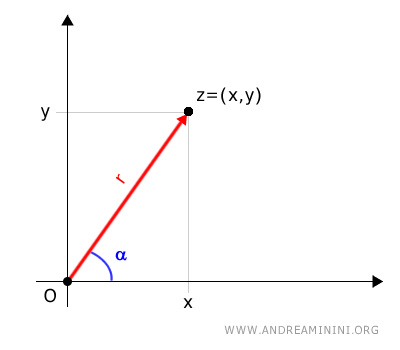
Le coordinate polari e le coordinate cartesiane sono due modi diversi per indicare un numero complesso.
Un esempio pratico
Il numero complesso z=2+3i
$$ z=2+3i $$
si trova alle coordinate cartesiane (2,3) del piano di Gauss.
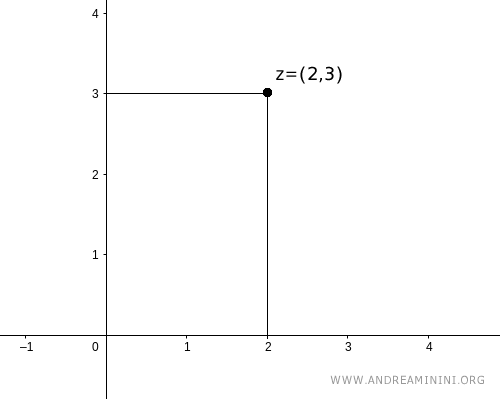
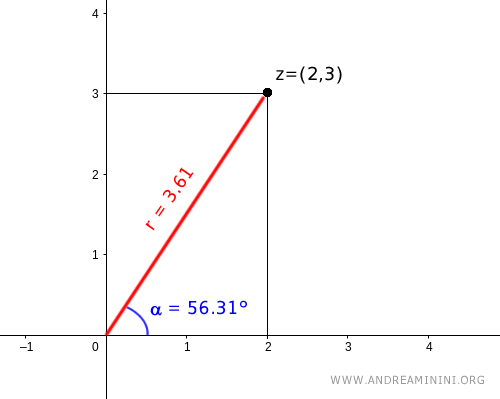
Il punto P alle coordinate (2,3) posso indicarlo usando le coordinate polari.
$$ z=P[r,\alpha] $$
Dove r=3.61 è la lunghezza del segmento OP mentre α=56.31° è l'angolo tra il segmento OP e l'asse polare orizzontale.
La dimostrazione
Ogni numero complesso z=x+yi è un punto di coordinate (x,y) sul piano di Gauss.
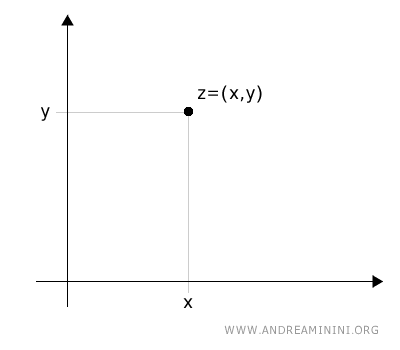
Nota. Tra i numeri complessi e i punti del piano c'è una corrispondenza biunivoca. In pratica per ogni numero complesso c'è uno e un solo punto del piano, e viceversa.
L'origine (O) del piano di Gauss la considero come il polo.
L'asse orizzontale positiva delle x, invece, lo considero come asse polare.
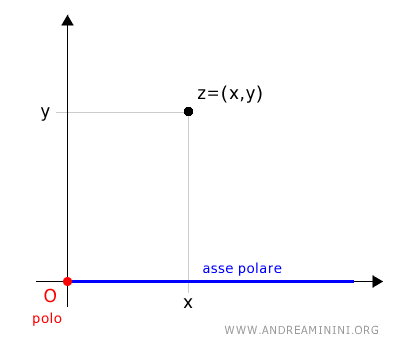
Quindi traccio un segmento orientato (vettore) che congiunge il polo (origine) con le coordinate cartesiane (a,b) del numero complesso.
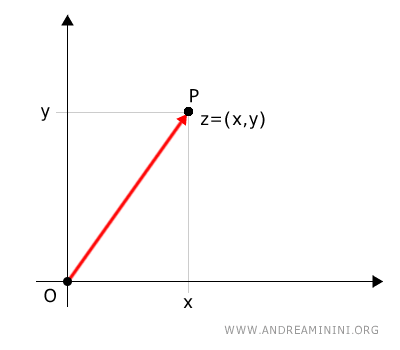
La lunghezza del segmento è una delle coordinate polari del numero. E' detta modulo del numero complesso.
Per indicare questa grandezza utilizzo la variabile r (raggio).
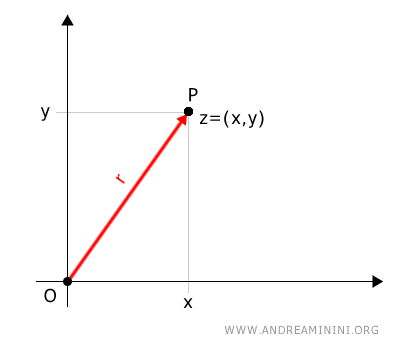
L'altra coordinata polare del numero complesso è l'angolo orientato alfa (α) tra l'asse polare e il segmento orientato, preso in senso antiorario.
L'angolo alfa è detto argomento del numero complesso.
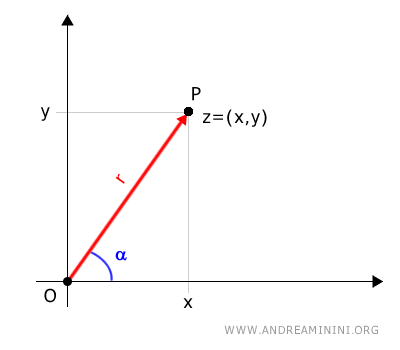
Quindi, le coordinate polari del numero sono P[r,α]
Ogni punto del piano ha coordinate polari diverse dagli altri punti.
Come trovare le coordinate polari di un numero complesso
Per calcolare le coordinate polari considero le coordinate cartesiane (x,y) del numero complesso.
$$ z = (x,y) $$
Dal punto di vista grafico
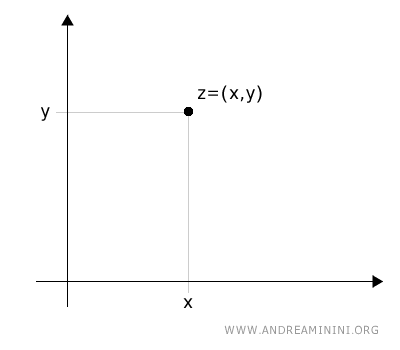
Il punto alle coordinate (x,y) forma un triangolo rettangolo OPA sul piano.
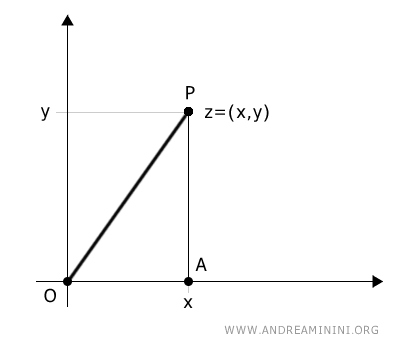
I lati del triangolo sono
$$ \overline{OP} = r $$ $$ \overline{OA} = x $$ $$ \overline{AP} = y $$
Per trovare la lunghezza del segmento OP uso il teorema di Pitagora.
$$ r = \overline{OP} = \sqrt{x^2+y^2} $$
Per trovare l'angolo, invece, studio il coefficiente angolare del segmento OP che è pari a al rapporto y/x
$$ \frac{ y }{ x } = \frac{ \overline{AP} }{ \overline{OA} } $$
Nota. Il segmento OP risiede su una retta r definita dall'equazione $$ y=mx+q $$ Il parametro q=0 in quanto la retta passa per l'origine. $$ y=mx $$ Ricavo il coefficiente angolare m $$ m = \frac{y}{x} $$ Dal punto di vista grafico
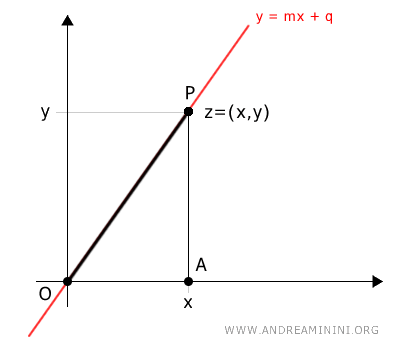
Secondo il primo teorema dei triangoli rettangoli
$$ x = r \cdot \cos \alpha $$ $$ y = r \cdot \sin \alpha $$
Quindi, il coefficiente angolare è
$$ \frac{ y }{ x } = \frac{ r \cdot \sin \alpha }{ r \cdot \cos \alpha } $$
Elimino r al numeratore e denominatore
$$ \frac{ y }{ x } = \frac{ \sin \alpha }{ \cos \alpha } $$
Sapendo che il rapporto tra seno e coseno di un angolo è la tangente sin(a)/cos(a)=tan(a).
$$ \frac{ y }{ x } = \tan \alpha $$
Per ottenere l'angolo alfa (α) applico l'arcotangente a entrambi i membri dell'equazione
$$ \arctan( \frac{ y }{ x } ) = \arctan( \tan \alpha ) $$
$$ \arctan( \frac{ y }{ x } ) = \alpha $$
Quindi, l'angolo alfa (argomento) è l'arcotangente del coefficiente angolare.
$$ \alpha = \arctan( \frac{ y }{ x } ) $$
Metodi alternativi per calcolare l'angolo. L'angolo alfa posso ottenerlo anche in altri modi. Ad esempio, dalle coordinate x tramite l'arcocoseno sapendo che $$ x = r \cdot \cos \alpha $$ $$ \frac{x}{r} = \cos \alpha $$ $$ \arccos(\frac{x}{r}) = \arccos( \cos \alpha) $$ $$ \arccos(\frac{x}{r}) = \alpha $$ In alternativa, dalle coordinate y tramite l'arcoseno sapendo che $$ y = r \cdot \sin \alpha $$ $$ \frac{y}{r} = \sin \alpha $$ $$ \arcsin( \frac{y}{r} ) = \arcsin( \sin \alpha ) $$ $$ \arcsin( \frac{y}{r} ) = \alpha $$
Esempio
Considero il numero complesso z=4+3i
$$ z = 4+3i $$
Le coordinate cartesiane sul piano di Gauss sono z=(4,3) ossia x=4 e y=3.
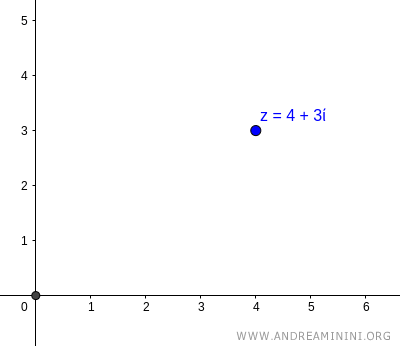
Traccio il segmento orientato che congiunge l'origine O (polo) con le coordinate cartesiane (4,3) del numero complesso.
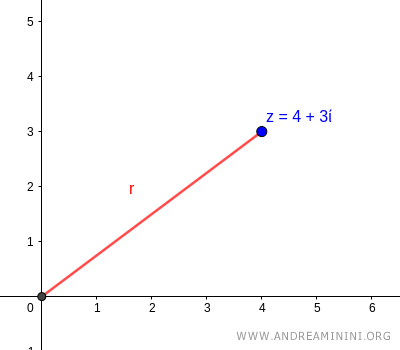
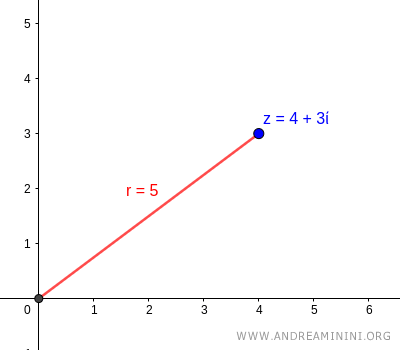
Per trovare la lunghezza (modulo) del vettore utilizzo il teorema di Pitagora
$$ r = \sqrt{x^2+y^2} $$
$$ r = \sqrt{4^2+3^2} $$
$$ r = \sqrt{16+9} $$
$$ r = \sqrt{25} $$
$$ r= 5 $$
Quindi il modulo del numero complesso è r=5
Per trovare l'angolo utilizzo l'arcotangente del coefficiente angolare y/x
$$ \alpha = \arctan( \frac{y}{x} ) $$
$$ \alpha = \arctan( \frac{3}{4} ) $$
$$ \alpha = \arctan( \frac{3}{4} ) $$
$$ \alpha = 36.87° $$
Quindi l'angolo (argomento) del numero complesso è 36.87°.
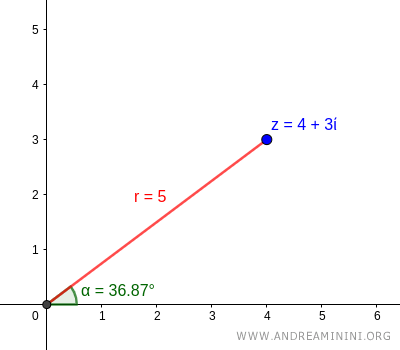
In conclusione, le coordinate polari P[r,α] del numero complesso z=4+3i sono
$$ P[ \ 5 \ , \ 36.87° \ ] $$
Come passare dalle coordinate polari alle coordinate cartesiane
Per passare dalle coordinate polari P[r,a] a quelle cartesiane (x,y) applico il primo teorema del triangolo rettangolo.
$$ x = r \cdot \cos \alpha $$ $$ y = r \cdot \sin \alpha $$
Il numero complesso in forma polare mi fornisce sia il modulo (r) che l'angolo alfa (argomento).
Sostituendo il modulo r e l'argomento alfa alle precedenti equazioni ottengo le coordinate cartesiane (x,y) del numero complesso.
Esempio
Considero il numero complesso z=4+3i in forma polare
$$ P[ \ 5 \ , \ 36.87° \ ] $$
Dal punto di vista grafico

Il modulo del numero complesso è r=5 mentre l'angolo è α=36.87°.
$$ r=5 $$
$$ \alpha = 36.87° $$
Secondo il primo teorema del triangolo rettangolo
$$ \begin{cases} x = r \cdot \cos \alpha \\ \\ y = r \cdot \sin \alpha \end{cases} $$
Sostituisco r=5 e α=36.87°.
$$ \begin{cases} x = 5 \cdot \cos 36.87° \\ \\ y = 5 \cdot \sin 36.87° \end{cases} $$
Poi calcolo il valore del seno e del coseno
Sapendo che sen(36.87°)=0.8 e cos(36.87°)=0.6
$$ \begin{cases} x = 5 \cdot 0.8 \\ \\ y = 5 \cdot 0.6 \end{cases} $$
Pertanto, le coordinate cartesiane del numero complesso sono
$$ \begin{cases} x = 4 \\ \\ y = 3 \end{cases} $$
Dal punto di vista grafico
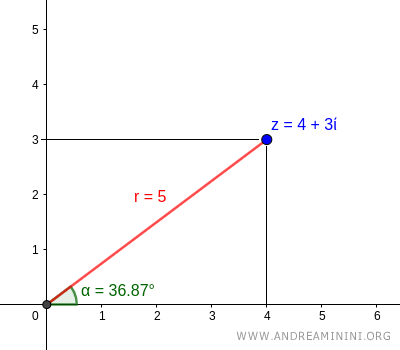
E così via.
