Come cambiare coordinate sul piano cartesiano

Il cambio di coordinate è il passaggio da un sistema di riferimento cartesiano RC a un altro RC'. $$ RC(O,i,j) \rightarrow RC'(O',i'.j') $$

Cos'è un riferimento cartesiano?

E' un riferimento cartesiano è un sistema composto da un'origine O, due vettori i,j e un prodotto scalare.

Esempio

I vettori i e j si intersecano nel punto O.

$$ i \begin{pmatrix} 1 \\ 0 \end{pmatrix} $$

$$ j \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

Essendo i due vettori dei vettori ortogonali a norma unitaria ( versori ), formano una base ortonormale (B).

$$ B = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} $$

La combinazione lineare dei vettori i,j della base con altrettanti scalari α₁, α₂ genera ogni vettore del piano.

$$ v = α_1 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + α_2 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

Esempio. In questo esempio i vettori i e j della base B generano tre vettori u, v, w del piano R².

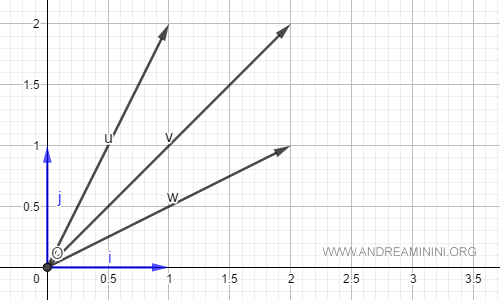
$$ u = \begin{pmatrix} 1 \\ 2 \end{pmatrix} = 1 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$ $$ v = \begin{pmatrix} 2 \\ 2 \end{pmatrix} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$ $$ w = \begin{pmatrix} 2 \\ 1 \end{pmatrix} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 1 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$ E così via.

E' facile dedurre che non esiste un solo riferimento cartesiano RC.

Ne esiste uno per ogni combinazione di vettori i e j.

Esistono infiniti riferimenti cartesiani RC del piano R² perché esistono infiniti vettori. E quindi, esistono infinite basi.

Come fare il cambio delle coordinate

Ogni riferimento cartesiano RC e RC' è associato a una base

$$ RC \rightarrow B $$

$$ RC' \rightarrow B' $$

Esempio. Sono due basi ortonormali $$ B = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} $$ $$ B' = \begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} $$ Ecco la rappresentazione grafica dei vettori delle due basi ortonormali B e B' associate ai riferimenti cartesiani RC e RC'.

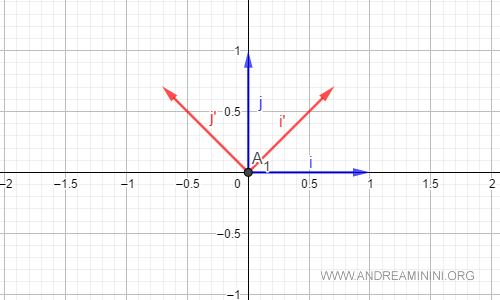
Per passare da una base all'altra si calcola la matrice di trasformazione.

$$ M_{B',B} $$

$$ M_{B,B'} $$

La prima matrice trasforma la base da B' a B.

La seconda matrice da B a B'.

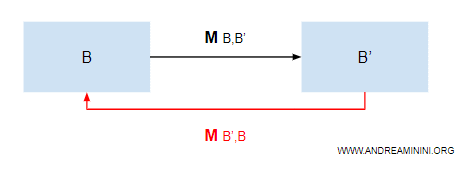
Quindi, ogni matrice di trasformazione è uguale alla matrice inversa dell'altra.

$$ M_{B',B} = M_{B,B'}^{-1} $$

$$ M_{B,B'} = M_{B',B}^{-1} $$

Esempio. Le matrici di trasformazione delle basi B e B' sono le seguenti $$ M_{B',B} = \begin{pmatrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} $$ $$ M_{B,B'} = M_{B',B}^{-1} = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} $$

Metodo alternativo

Le basi dei riferimenti cartesiani sono basi ortonormali, sono composte soltanto da vettori ortogonali a norma unitaria ( versori ).

Quindi, le matrici di trasformazione delle basi sono anche matrici ortogonali.

Nel caso delle matrici ortogonali, ogni matrice di trasformazione è anche uguale alla matrice trasposta dell'altra.

$$ M_{B',B} = M_{B,B'}^T $$

$$ M_{B,B'} = M_{B',B}^T $$

E' un modo più semplice e rapido per calcolarle.

Esempio. Le matrici di trasformazione delle basi B e B' sono le seguenti $$ M_{B',B} = \begin{pmatrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} $$ $$ M_{B,B'} = M_{B',B}^{T} = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} $$ Il risultato è lo stesso.

Pertanto, il prodotto di una matrice di trasformazione M_B',B per la sua trasposta M^T_B',B genera una matrice identità.

$$ M_{B',B} \cdot M_{B',B}^T = I_n $$

$$ M_{B,B'} \cdot M_{B,B'}^T = I_n $$

Lo stesso si può dire per il prodotto per una matrice di trasformazione per l'altra matrice di trasformazione.

$$ M_{B',B} \cdot M_{B,B'} = I_n $$

$$ M_{B,B'} \cdot M_{B',B} = I_n $$

Esempio. Ecco il prodotto di una matrice di trasformazione per l'altra $$ M_{B',B} \cdot M_{B,B'} = \begin{pmatrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} \cdot \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} $$ Questo si verifica perché, in questo caso specifico la matrice trasposta è uguale alla matrice inversa (M^T=M^-1) e il prodotto di qualsiasi matrice quadrata M per la sua matrice inversa M^-1 è sempre uguale a una matrice identità I $$ M \cdot M^{-1} = I $$

Il determinante della matrice di trasformazione

Essendo matrici ortonormali, il determinante di ogni matrice di trasformazione può essere uguale a +1 oppure a -1.

Esempio. Il determinante della matrice di trasformazione M_B',B è uguale a 1. $$ det ( M_{B',B} ) = \begin{vmatrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{vmatrix} = \frac{1}{2} + \frac{1}{2} = 1 $$

Il segno del determinante è molto importante, perché permette di capire se due basi sono equiverse o contraverse.

I riferimenti cartesiani equiversi e contraversi

• Due riferimenti cartesiani sono detti equiversi se le basi danno la stessa orientazione al piano ( basi equiverse ). $$ det(M_{B',B}) = det(M_{B,B'}) = +1 $$
• Due riferiemnti cartesiani sono detti contraversi se le basi danno un'orientazione opposta al piano ( basi contraverse ). $$ det(M_{B',B}) = det(M_{B,B'}) = -1 $$

Esempi

Ho tre basi

$$ B = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} $$

$$ B' = \begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} $$

$$ B'' = \begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} $$

Le basi B e B' ( blu e rossa ) danno la stessa orientazione al piano.

Viceversa, la base B" ( verde ) dà un'orientazione opposta al piano.

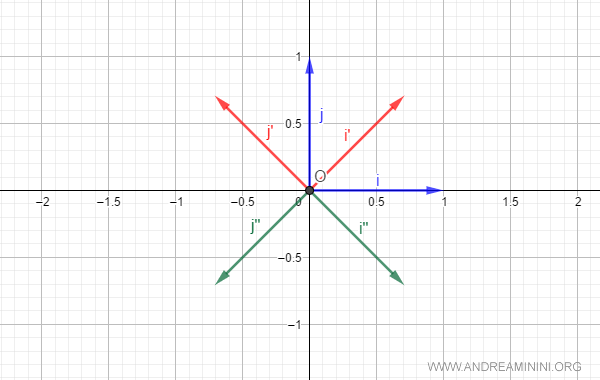
Pertanto, le basi B e B' ( blu e rossa ) sono tra loro basi equiverse.

Il determinante della matrice di trasformazione M_B'B è uguale a +1.

$$ det ( M_{B',B} ) = \begin{vmatrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{vmatrix} = \frac{1}{2} + \frac{1}{2} = 1 $$

Viceversa, le basi B e B'' ( blu e verde ) sono tra loro basi contraverse.

Il determinante della matrice di trasformazione M_B''B è uguale a -1.

$$ det ( M_{B'',B'} ) = \begin{vmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{vmatrix} = - \frac{1}{2} - \frac{1}{2} = -1 $$

La matrice di rotazione

Basi equiverse

Se il cambio di base è tra due basi equiverse, allora l'angolo di rotazione θ tra i vettori i e i' delle due basi soddisfa la seguente condizione:

$$ i' = (\cos θ) \cdot i + (\sin θ) \cdot j $$

$$ j' = (- \sin θ) \cdot i + (\cos θ) \cdot j $$

Per una spiegazione geometrica delle precedenti formule rimando a una dimostrazione che ho scritto a parte.

Esempio. I vettori della base canonica sono $$ i = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \: \: \: j = \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$ Per fare una rotazione di 180° ( π rad. ). $$ i' = (\cos π) \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + (\sin π) \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} = -1 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 0 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} -1 \\ 0 \end{pmatrix} $$ $$ j' = (- \sin π) \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + (\cos π) \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} = 0 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} -1 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ -1 \end{pmatrix} $$ Dal punto di vista grafico, ecco la rotazione di 180°

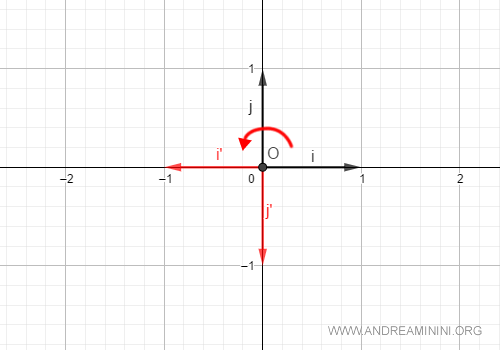
Quindi la matrice di rotazione dell'angolo θ in senso antiorario è

$$ M_{B',B}(θ) = \begin{pmatrix} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{pmatrix} $$

Basi contraverse

Se il cambio di base è tra due basi contraverse, allora l'angolo di rotazione θ tra i vettori i e i' delle due basi soddisfa la seguente condizione:

$$ i' = (\cos θ) \cdot i + (\sin θ) \cdot j $$

$$ j' = (\sin θ) \cdot i - ( \cos θ) \cdot j $$

Esempio. I vettori della base canonica sono $$ i = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \: \: \: j = \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$ Per fare una rotazione di 180° ( π rad. ) tra basi contraverse. $$ i' = (\cos π) \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + ( \sin π) \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} = -1 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 0 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} -1 \\ 0 \end{pmatrix} $$ $$ j' = (\sin π) \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + ( - \cos π) \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} = 0 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} +1 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$ Dal punto di vista grafico, ecco la rotazione di 180°

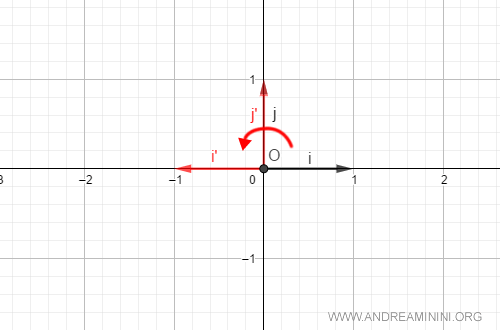
Quindi la matrice di rotazione dell'angolo θ in senso antiorario con riflessione rispetto all'asse x è

$$ M_{B',B}(θ) = \begin{pmatrix} \cos θ & \sin θ \\ \sin θ & - \cos θ \end{pmatrix} $$

A cosa servono le matrici di rotazione?

Permettono di trasformare le coordinate di un punto da un riferimento cartesiano RC a un altro RC' tramite le seguenti formule di trasformazione.

$$ C_{RC'}(P) = M_{B,B'} \cdot C_{RC}(P) + C_{RC'}(O) $$ $$ C_{RC}(P) = M_{B',B} \cdot C_{RC'}(P) + C_{RC}(O') $$

Dove C sono le coordinate di un punto in un particolare riferimento cartesiano.

Nel passaggio da un riferimento cartesiano a un altro

• La matrice di rotazione M determina la rotazione del piano sull'origine O del riferimento cartesiano di partenza.
• Le coordinate C(O) determinano la traslazione del piano al punto di origine del riferimento cartesiano di destinazione.

Esempio

Ho due basi equiverse B e B' (rossa) che, per semplicità, hanno in comune la stessa origine O.

I due riferimenti cartesiani si distinguono solo per una rotazione di 180° ( 1 π radiante ).

La matrice di trasformazione da B' a B è la seguente:

$$ M_{B',B}(θ) = \begin{pmatrix} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} $$

Ho un punto P' con coordinate (1,1) sul RC' ( rosso ).

$$ P' \begin{pmatrix} 1 \\ 1 \end{pmatrix} $$

Il piano RC è ruotato di 180°, quindi il punto P' si trova nel quadrante in basso a sinistra.

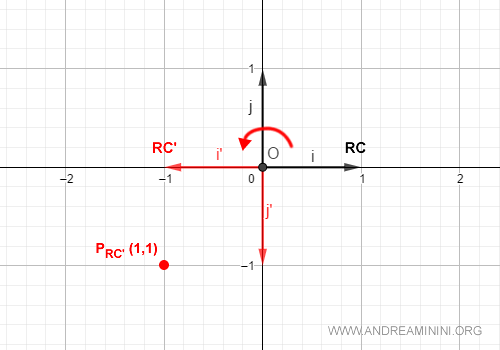
Voglio trovare le coordinate del punto sull'altro riferimento cartesiano RC ( nero ).

Pertanto, utilizzo la formula di trasformazione.

$$ C_{RC}(P) = M_{B',B} \cdot C_{RC'}(P) + C_{RC}(O') $$

La matrice di trasformazione già la conosco

$$ C_{RC}(P) = \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} \cdot C_{RC'}(P) + C_{RC}(O') $$

So anche che i due riferimenti cartesiani hanno la stessa origine O.

Quindi, l'ultima componente è il punto (0,0).

$$ C_{RC}(P) = \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} \cdot C_{RC'}(P) + \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

Nota. Se l'origine fosse diversa avrei dovuto tradurre le coordinate del punto di origine O' del piano di partenza in quelle del piano di destinazione. In pratica, avrei dovuto traslare il punto di origine degli assi.

A questo punto devo indicare il punto P(1,1) del piano RC' da tradurre nelle coordinate dell'altro piano.

$$ C_{RC}(P) = \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

Svolgo i calcoli matriciali/vettoriali e ottengo le coordinate del punto P nell'altro riferimento cartesiano.

$$ C_{RC}(P) = \begin{pmatrix} -1 \\ -1 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

$$ C_{RC}(P) = \begin{pmatrix} -1 \\ -1 \end{pmatrix} $$

Le coordinate del punto P' sul riferimento cartesiano RC sono (-1,-1)

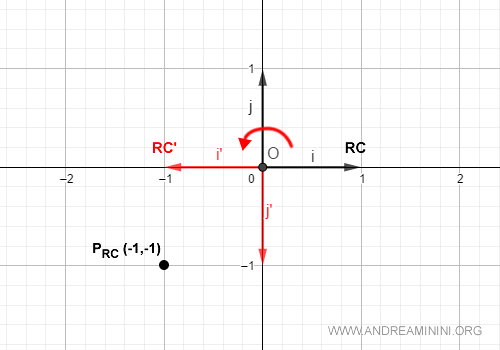
E così via

Verifica. Per fare il procedimento inverso devo usare la matrice di trasformazione inversa M_B',B^-1=M_B,B' che, come già visto, è uguale alla trasposta M_B',B^T. In questo caso particolare le due matrici di trasformazione sono identiche M_B',B=M_B,B'. Quindi $$ C_{RC'}(P) = M_{B,B'} \cdot C_{RC}(P) + C_{RC'}(O) $$ $$ C_{RC'}(P) = \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} -1 \\ -1 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$ $$ C_{RC'}(P) = \begin{pmatrix} 1 \\ 1 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$ $$ C_{RC'}(P) = \begin{pmatrix} 1 \\ 1 \end{pmatrix} $$ Ottengo così le coordinate del punto sul piano di riferimento di partenza RC'.