La base ortonormale
Una base dello spazio vettoriale B{v,w} è detta base ortonormale se è composta da vettori ortogonali $$ <v,w>=0 \:\:se\:\: v \ne w $$ e a norma unitaria $$ || \vec{v} || = || \vec{w} || = 1 $$
In altre parole, le condizioni di una base ortonormale sono due
- I vettori della base hanno norma unitaria ossia un modulo (lunghezza) uguale a 1.
- I vettori della base sono diversi e ortogonali tra loro, in questi casi il loro prodotto scalare <v,w>=0 è nullo.
Nota. I vettori delle basi ortonormali sono anche detti vettori a norma unitaria perché la norma dei due vettori è uguale a 1. $$ ||v|| = 1 $$ $$ ||w|| = 1 $$ Quest'ultima proprietà si deduce dal prodotto scalare unitario <v,w>=1 nel caso in cui i vettori v e w siano uguali. Qualsiasi norma indotta dal prodotto scalare è $$ ||v|| = \sqrt{ <v,v> } $$ Spesso viene aggiunta anche questa condizione. Se i vettori della base sono uguali v=w il loro prodotto scalare <v,w>=1 deve essere uguale a 1.
Esempio di base ortonormale
Questa base è un esempio pratico di base ortonormale.
Si tratta di una base canonica.
$$ B = \{ \vec{v_1} \ , \ \vec{v_2} \} = \{ \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \begin{pmatrix} 0 \\ 1 \end{pmatrix} \} $$
Entrambi i vettori sono a norma unitaria.
$$ ||\vec{v}|| = \sqrt{1^2+0^2} = 1 $$
$$ ||\vec{w}|| = \sqrt{0^2+1^2} = 1 $$
I due vettori della base sono diversi e il loro prodotto scalare è nullo.
$$ <v,w>= ( 1 \cdot 0 ) + ( 0 \cdot 1 ) = 0+0 = 0 $$
Quindi, è una base ortonormale.
Dal punto di vista grafico i due vettori formano un angolo di 90° (vettori ortogonali) e hanno una lunghezza (modulo) pari a 1.
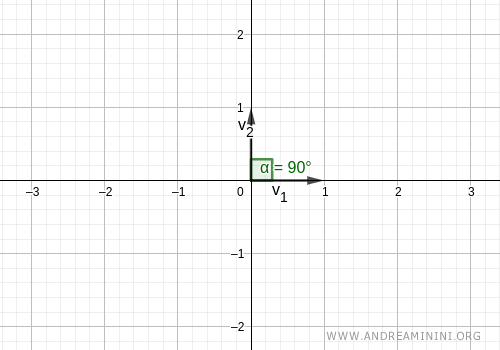
Nota. In una base ortonormale i vettori sono vettori a norma unitaria. E' un altro modo per verificare l'ortonormalità della base. $$ ||v|| = \sqrt{1^2+0^2}=1 $$ $$ ||w|| = \sqrt{0^2+1^2}=1 $$
La differenza tra basi ortogonali e ortonormali
Una base ortonormale è sempre anche una base ortogonale perché è composta da vettori ortogonali.
Non vale però l'inverso. Una base ortogonale non è detto che sia anche una base ortornormale.
Esempio
Questa base è ortogonale perché
$$ B = \{ \begin{pmatrix} 1 \\ -1 \end{pmatrix} , \begin{pmatrix} 1 \\ 1 \end{pmatrix} \} $$
perché sono due vettori diversi e il prodotto scalare è nullo
$$ <v,w>= ( 1 \cdot 1 ) + ( -1 \cdot 1 ) = 1-1 = 0 $$
Pertanto, i due vettori formano un angolo di 90° ossia sono vettori ortogonali
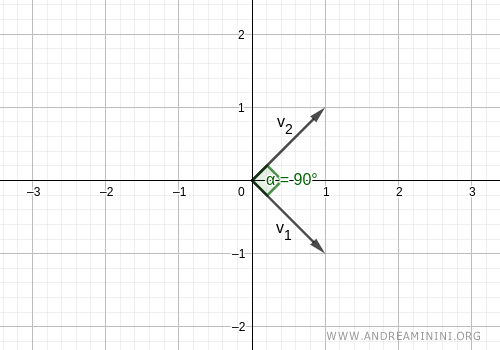
Tuttavia, non è anche una base ortonormale perché i vettori non sono tutti a norma unitaria.
$$ ||v_1|| = \sqrt{1^2+(-1)^2}=\sqrt{2} $$ $$ ||v_2|| = \sqrt{1^2+1^2}=\sqrt{2} $$
Dal punto di vista grafico questo vuol dire che la lunghezza (modulo) dei vettori è diversa da 1.
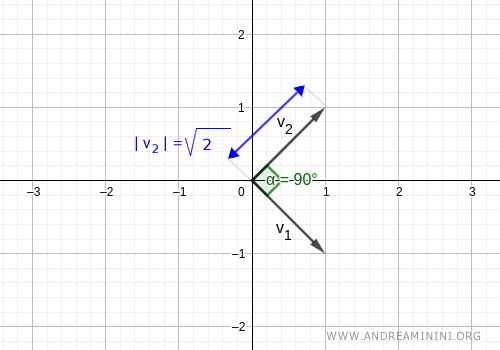
Pur formando un angolo di 90° (vettori ortogonali) non sono anche ortonormali.
Nota. Qualsiasi base ortogonale può comunque essere trasformata in base ortonormale tramite la normalizzazione dei vettori che compongono la base. Per un approfondimento vedere come trasformare una base ortogonale in ortonormale.
