Errore standard nell'interpolazione

L'errore standard nell'interpolazione misura la differenza tra i valori interpolati (stimati) e i valori reali (osservati) di una funzione o di un dataset.  $$ E = \sqrt{\frac{1}{n} \cdot \sum_{i=1}^{n} (f(x_i) - \hat{f}(x_i))^2} $$ Dove \( f(x_i) \) sono i valori reali della funzione, \( \hat{f}(x_i) \) sono i valori interpolati e \( n \) è il numero di punti dati.

E' uno dei principali indici di scostamento dell'interpolazione.

Questo valore rappresenta una misura della deviazione quadratica media tra i valori osservati e quelli stimati tramite interpolazione.

L'errore standard sarà tanto più piccolo quanto migliore sarà l'interpolazione.

Nota. L'errore standard viene utilizzato per valutare l'accuratezza di un metodo di interpolazione, come l'interpolazione lineare, polinomiale o spline. Tuttavia, l'errore può dipendere dalla scelta dei nodi di interpolazione e dalla regolarità della funzione da interpolare. Inoltre, non considera se i valori confrontati sono grandi o piccoli. Spesso, al suo posto si preferisce usare l'indice quadratico medio.

Un esempio pratico

Considero un insieme di dati $ x $ e $ y $

x	y
1	2
2	3
3	5
4	4
5	6

Questi $ n = 5 $ punti osservati sono sparpagliati sul piano.

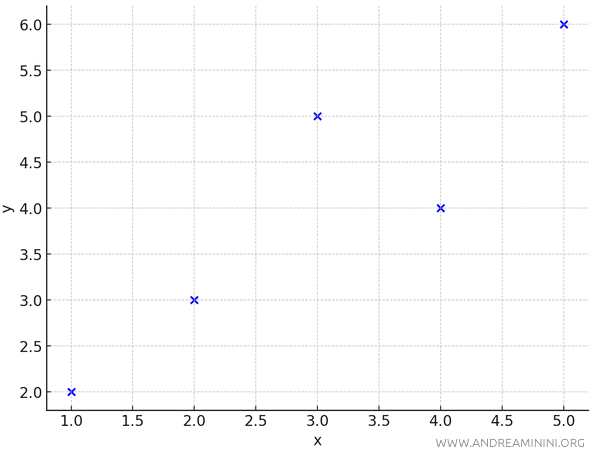
Per interpolarli utilizzo la retta \(y = 0.9x + 1.3\).

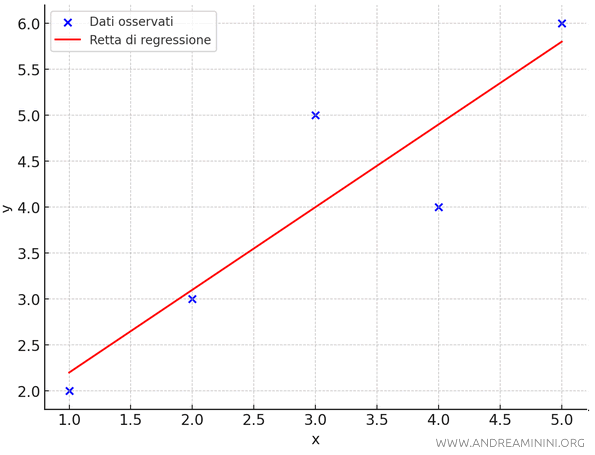
A questo punto voglio calcolare l'errore standard dell'interpolazione.

Per prima cosa, determino gli errori parziali $ e_i = y_i - y_{\text{previsti}}(x_i) $, ossia i residui, cioè la differenza tra i valori osservati \( y \) e i valori previsti \( y_{\text{previsti}} \) tramite la retta \(y = 0.9x + 1.3\).

Questo passo serve a misurare quanto ciascun punto dei dati si discosta dalla funzione di accostamento (interpolazione).

x	y	yprevisto	e = y - yprevisto
1	2	2.2	-0.2
2	3	3.1	-0.1
3	5	4.0	1.0
4	4	4.9	-0.9
5	6	5.8	0.2

Elevo al quadrato i residui  $ e_i^2 = [y_i - y_{\text{previsti}}(x_i)]^2 $ per evitare che gli errori negativi e positivi si annullino tra loro.

x	y	yprevisto	e = y - yprevisto	e2
1	2	2.2	-0.2	0.04
2	3	3.1	-0.1	0.01
3	5	4.0	1.0	1.00
4	4	4.9	-0.9	0.81
5	6	5.8	0.2	0.04

Poi sommo i quadrati degli errori per ottenere la somma totale degli errori parziali:

$$ \sum_{i=1}^{n} (f(x_i) - \hat{f}(x_i))^2  = \sum_{i=1}^{n} e^2 = 0.04 + 0.01 + 1.00 + 0.81 + 0.04 = 1.90 $$

A questo punto posso calcolare l'errore standard (E).

$$ E = \sqrt{\frac{1}{n} \cdot \sum_{i=1}^{n} (f(x_i) - \hat{f}(x_i))^2} $$

Sapendo che la somma dei quadrati degli errori è 1.90 e che il numero totale di punti osservati è \(n = 5\).

$$ E = \sqrt{\frac{1}{n} \cdot \underbrace{ \sum_{i=1}^{n} (f(x_i) - \hat{f}(x_i))^2}_{1.90} } $$

$$ E = \sqrt{\frac{1}{5} \cdot 1.90 } $$

$$ E = \sqrt{ 0.38 } $$

$$ E =  0.616 $$

Quindi, l'errore standard è \( 0.616 \), che rappresenta una misura della deviazione media dei punti dai valori previsti dalla retta di regressione.

E così via.