Interpolazione lineare
Una funzione interpolante lineare è una funzione che approssima una serie di punti dati \( (x_i, y_i) \) con una retta.
L'obiettivo dell'interpolazione lineare è trovare una retta che "passi attraverso" o sia il più vicina possibile a questi punti, minimizzando la distanza complessiva tra la retta e i punti.
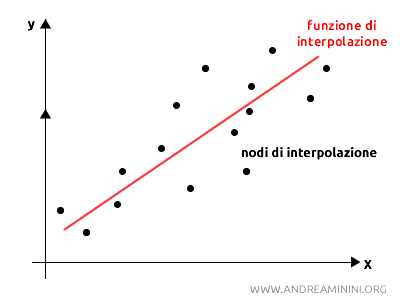
Come si calcola la retta di interpolazione
Se ho un insieme di punti \( (x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n) \), la funzione interpolante lineare è una retta della forma:
$$ y = ax + b $$
Dove \( a \) è la pendenza della retta e \( b \) è l'intercetta sull'asse delle ordinate.
Devo determinare i coefficienti \( a \) e \( b \) in modo tale che la retta descriva al meglio la tendenza dei dati.
Per farlo, minimizzo la somma dei quadrati delle differenze tra i valori effettivi \( y_i \) e i valori previsti dalla retta \( ax_i + b \) tramite la tecnica detta metodo dei minimi quadrati.
$$ S(a; b) = \sum_{i=1}^{n} (y_i - ax_i - b)^2 $$
L'equazione della retta interpolante che minimizza la somma dei quadrati delle differenze è la seguente:
$$ y - \bar{y} = a(x - \bar{x}) $$
Dove \( \bar{x} \) è la media dei valori della variabile indipendente $ x $ mentre $ \bar{y} $ è la media dei valori della variabile dipendente $ y $.
$$ \bar{x} = \frac{1}{n} \cdot \sum_{i=1}^n x_i $$
$$ \bar{y} = \frac{1}{n} \cdot \sum_{i=1}^n y_i $$
Il punto \( (\bar{x} ; \bar{y} ) \) è detto "baricentro" della distribuzione dei dati ed il punto medio delle coordinate \( x \) e \( y \) in cui passa la retta interpolante.
La formula per calcolare il coefficiente \( a \), che rappresenta la pendenza della retta, è data da:
$$ a = \frac{ \sum_{i=1}^n (x_i-\bar{x}) \cdot (y_i-\bar{y}) }{ \sum_{i=1}^n {(x_i-\bar{x})^2} } $$
Il risultato finale è una retta di regressione lineare che meglio approssima un insieme di punti.
Un esempio pratico
Considero una distribuzione composta da $ n=4 $ punti (x;y) noti.
| x | y |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Questi punti sono sparpagliati nel piano cartesiano nell'intervallo (1,4).
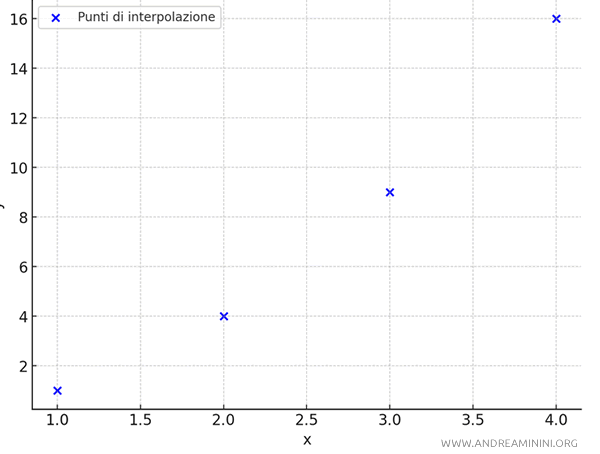
Per trovare una retta che approssima i dati in modo continuo, utilizzo l'equazione della funzione interpolante.
$$ y - \bar{y} = a(x - \bar{x}) $$
Calcolo le medie delle variabili x e y.
$$ \bar{x} = \frac{1+2+3+4}{4} = \frac{10}{4} $$
$$ \bar{y} = \frac{1+4+9+16}{4} = \frac{30}{4} $$
Sostituisco i valori delle medie $ \bar{x} =\frac{10}{4} $ e $ \bar{y} = \frac{30}{4} $ nell'equazione della retta interpolante.
$$ y - \bar{y} = a(x - \bar{x}) $$
$$ y - \frac{30}{4} = a(x - \frac{10}{4} ) $$
A questo punto calcolo il coefficiente $ a $ che determina la pendenza della retta usando la formula:
$$ a = \frac{ \sum_{i=1}^n (x_i-\bar{x}) \cdot (y_i-\bar{y}) }{ \sum_{i=1}^n {(x_i-\bar{x})^2} } $$
Sapendo che i dati sono $ n=4 $ e le medie sono $ \bar{x} =\frac{10}{4} $ e $ \bar{y} = \frac{30}{4} $
$$ a = \frac{ \sum_{i=1}^4 (x_i- \frac{10}{4}) \cdot (y_i- \frac{30}{4} ) }{ \sum_{i=1}^4 {(x_i- \frac{10}{4})^2} } $$
Questa tabella riassume i calcoli per ciascun punto \( (x_i, y_i) \), mostrando le differenze rispetto alle medie, i prodotti di queste differenze, e i quadrati delle differenze di \( x_i \).
$$
\begin{array}{|c|c|c|c|c|c|}
\hline
x_i & y_i & x_i - \bar{x} & y_i - \bar{y} & (x_i - \bar{x})(y_i - \bar{y}) & (x_i - \bar{x})^2 \\
\hline
1 & 1 & -1.5 & -6.5 & 9.75 & 2.25 \\
2 & 4 & -0.5 & -3.5 & 1.75 & 0.25 \\
3 & 9 & 0.5 & 1.5 & 0.75 & 0.25 \\
4 & 16 & 1.5 & 8.5 & 12.75 & 2.25 \\
\hline
\end{array}
$$
Sostituisco il risultato nella formula per calcolare il coefficiente \( a \):
$$ a = \frac{ 9.75+1.75+0.75+12.75 }{ 2.25+0.25+0.25+2.25 } $$
$$ a = \frac{25}{5} = 5 $$
Ho trovato che la pendenza \( a \) è 5.
Sostituisco il coefficiente $ a=5 $ nell'equazione della retta interpolante:
$$ y - \frac{30}{4} = a(x - \frac{10}{4} ) $$
$$ y - \frac{30}{4} = 5(x - \frac{10}{4}) $$
$$ y = 5x - 5 \cdot \frac{10}{4} + \frac{30}{4}$$
$$ y = 5x - \frac{50}{4} + \frac{30}{4}$$
$$ y = 5x + \frac{30-50}{4} $$
$$ y = 5x - \frac{20}{4} $$
$$ y = 5x - 5 $$
Quindi l'equazione della retta è:
$$ y = 5x - 5 $$
Questa è la retta che approssima i dati usando il metodo dei minimi quadrati.
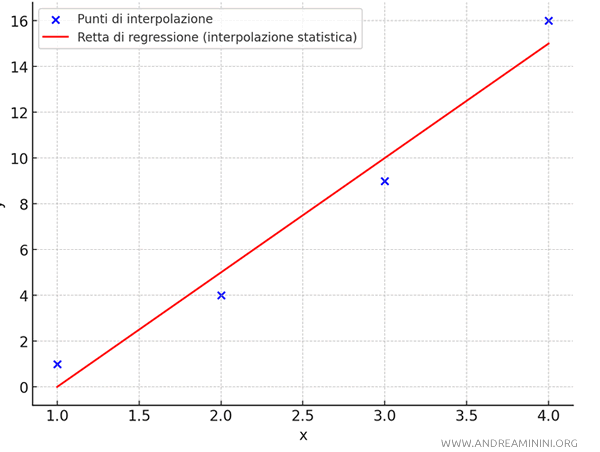
Nota. La retta interpolante $ y = 5x - 5 $ passa tra i punti minimizzando le distanze e attraversa il punto \( (\bar{x} ; \bar{y} ) = ( \frac{10}{4} ; \frac{30}{4} ) = (2.5; 7.5 ) \) detto baricentro della distribuzione.
E così via.
