Indice quadratico relativo
L'indice quadratico relativo è una misura utilizzata per valutare la precisione di un modello di interpolazione o regressione. È definito come il rapporto tra l'errore standard (E) e la media dei valori teorici f(x). $$ I = \frac{ E }{\frac{1}{n} \sum_{i=1}^{n} f(x_i)} $$
Sapendo che l'errore standard (E) è calcolato come la radice quadrata della media dei quadrati delle differenze tra i valori osservati \( y_i \) e i valori stimati \( f(x_i) \), la formula dell'indice quadratico relativo è la seguente:
$$ I = \frac{\sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - f(x_i))^2}}{\frac{1}{n} \sum_{i=1}^{n} f(x_i)} $$
Dove \( y_i \) sono i valori osservati, \( f(x_i) \) sono i valori stimati dalla funzione, \( n \) è il numero di osservazioni.
Questo indice è un valore non negativo che mi consente di confrontare l'accuratezza del modello tenendo conto della scala dei dati.
Mi permette di valutare se l'approssimazione fornita dalla funzione è accettabile rispetto ai valori reali oppure no.
Nota. Quanto più l'indice è vicino a zero, tanto più accurata è l'approssimazione. Generalmente, viene considerata accettabile una misura al di sotto di $ I<0.1 $. Va comunque considerato che il livello di accettazione cambia a seconda delle circostanze e delle esigenze di accuratezza della stima. Quindi, a volte la soglia è più alta, altre volte è più bassa.
Un esempio pratico
Prendo in considerazione un insieme di dati $ x $ e $ y $ composto da $ n=5 $ osservazioni.
| x | y |
|---|---|
| 1 | 2 |
| 2 | 3 |
| 3 | 5 |
| 4 | 4 |
| 5 | 6 |
Questi dati sono rappresentati come punti sparpagliati nel piano.
Calcolo una retta di interpolazione \(y = 0.9x + 1.3\) per stimare i punti intermedi in modo continuo.
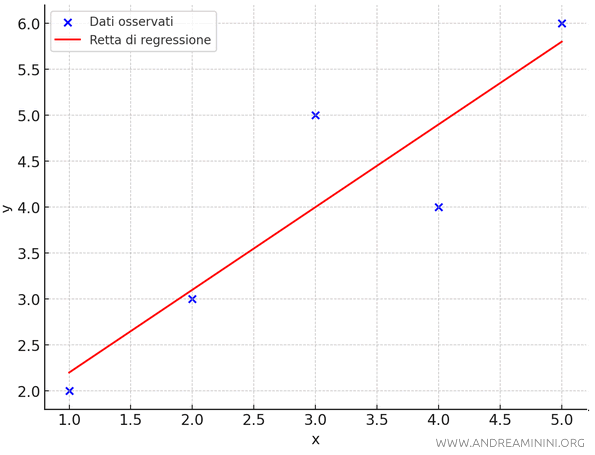
L'errore standard dell'interpolazione lo ottengo osservando gli errori parziali $ e_i = y_i - f(x) $, ossia la differenza tra i valori osservati \( y \) e i valori previsti \( f(x) \) tramite la retta di interpolazione \(f(x) = 0.9x + 1.3\).
| x | y | f(x) | e = y - f(x) |
|---|---|---|---|
| 1 | 2 | 2.2 | -0.2 |
| 2 | 3 | 3.1 | -0.1 |
| 3 | 5 | 4.0 | 1.0 |
| 4 | 4 | 4.9 | -0.9 |
| 5 | 6 | 5.8 | 0.2 |
Elevo al quadrato i residui $ e_i^2 = [y_i - f(x)]^2 $ per evitare la compensazione tra gli errori negativi e positivi.
| x | y | f(x) | e = y - f(x) | e2 |
|---|---|---|---|---|
| 1 | 2 | 2.2 | -0.2 | 0.04 |
| 2 | 3 | 3.1 | -0.1 | 0.01 |
| 3 | 5 | 4.0 | 1.0 | 1.00 |
| 4 | 4 | 4.9 | -0.9 | 0.81 |
| 5 | 6 | 5.8 | 0.2 | 0.04 |
La somma dei quadrati degli errori parziali è 1.90.
$$ \sum_{i=1}^{n} (f(x_i) - \hat{f}(x_i))^2 = \sum_{i=1}^{n} e^2 = 0.04 + 0.01 + 1.00 + 0.81 + 0.04 = 1.90 $$
Quindi, l'errore standard (E) dell'interpolazione è la seguente:
$$ E = \sqrt{\frac{1}{n} \cdot \sum_{i=1}^{n} (f(x_i) - \hat{f}(x_i))^2} $$
So già che la somma dei quadrati degli errori è 1.90 e che il numero dei dati osservati è \(n = 5\).
$$ E = \sqrt{\frac{1}{n} \cdot \underbrace{ \sum_{i=1}^{n} (f(x_i) - \hat{f}(x_i))^2}_{1.90} } $$
$$ E = \sqrt{\frac{1}{5} \cdot 1.90 } $$
$$ E = \sqrt{ 0.38 } $$
$$ E = 0.616 $$
Quindi, l'errore standard è \( 0.616 \).
Una volta trovato l'errore standard, posso calcolare l'indice quadratico medio.
$$ I = \frac{ E }{\frac{1}{n} \sum_{i=1}^{n} f(x_i)} $$
Sostituisco E=0.616 e n=5.
$$ I = \frac{ 0.616 }{\frac{1}{n} \sum_{i=1}^{n} f(x_i)} $$
La media dei valori teorici ottenuti tramite la funzione \(f(x) = 0.9x + 1.3\) è 4.
$$ \frac{1}{n} \sum_{i=1}^{n} f(x_i) = \frac{1}{5} \cdot (2.2+3.1+4.0+4.9+5.8) = \frac{20}{5} = 4 $$
Infine, sostituisco la media dei valori teorici nella formula dell'indice quadratico medio.
$$ I = \frac{ 0.616 }{4} = 0.154 $$
Quindi, in questo esempio l'indice quadratico medio dell'interpolazione è 0.154.
Quali valori sono accettabili?
L'indice quadratico relativo \( I \) può assumere valori non negativi, poiché è il rapporto tra due quantità sempre positive: l'errore standard (che è una radice quadrata) e la media dei valori teorici che, per convenzione, è considerata positiva.
Quindi, l'indice è sempre maggiore o uguale a zero.
$$ I \geq 0 $$
In generale i valori vicini a 0 indicano che l'errore del modello è molto piccolo rispetto alla scala dei valori teorici, quindi il modello è molto preciso.
I valori maggiori 0 indicano che c'è una certa discrepanza tra i valori osservati e quelli teorici.
Più il valore di \( I \) aumenta, maggiore è l'errore relativo.
In pratica, in base al contesto si considerano spesso soglie specifiche per valutare la bontà del modello.
Ad esempio, un valore di \( I \) pari o inferiore a 0,1 può indicare un'approssimazione molto buona, mentre valori più alti potrebbero suggerire la necessità di un miglioramento del modello o di una funzione di interpolazione più precisa.
E così via.
