Il metodo dei minimi quadrati

Il metodo dei minimi quadrati mi permette di individuare i parametri della funzione interpolante che minimizza la somma dei quadrati degli errori relativi.

In altre parole, dati una serie di punti (x₁;y₁), (x₂;y₂),... , questo metodo trova il coefficiente angolare e l'intercetta di una retta $ y = mx+q $ che passa tra i punti riducendo al minimo la somma dei quadrati degli errori relativi.

$$ S = \sum_{i=1}^n e^2_i = \sum_{i=1}^n [y_i - f(x_i)]^2 $$

Questo metodo viene impiegato principalmente nella regressione lineare per stimare i parametri di una funzione lineare o di un altro tipo di modello di relazione tra variabili.

Nota. In generale, posso usarlo anche per trovare una curva (anziché una retta) che meglio approssima un insieme di dati osservati, minimizzando la somma dei quadrati delle differenze (distanze verticali) tra i valori osservati e quelli previsti dal modello.

Come funziona il metodo dei minimi quadrati

Considero un insieme di punti \( (x_i, y_i) \) per \( i = 1, 2, \dots, n \), devo trovare i parametri \( m \) e \( q \) che minimizzano la seguente funzione obiettivo:

$$ y = mx + q $$

Dove \(y\) è la variabile dipendente, \(x\) è la variabile indipendente, \(m\) è il coefficiente angolare della retta, e \(q\) è l'intercetta.

In questo caso si tratta di una funzione lineare ossia di una retta.

I parametri \(m\) e \(q\) sono determinati in modo tale da minimizzare l'errore, misurato come la somma dei quadrati delle differenze tra i valori osservati \(y_i\) e i valori previsti \(y_{\text{previsti}}\).

$$ S(m, b) = \sum_{i=1}^{n} \left( y_i - (mx_i + b) \right)^2 $$

Ad esempio, utilizzo la procedura per la regressione lineare.

Per prima cosa calcolo il coefficiente angolare \( m \)_

$$ m = \frac{n \sum (x_i y_i) - \sum x_i \sum y_i}{n \sum x_i^2 - (\sum x_i)^2} $$

Dove:

• \(n\) è il numero di punti,
• \(\sum x_i\) è la somma di tutti i valori di \(x\),
• \(\sum y_i\) è la somma di tutti i valori di \(y\),
• \(\sum x_i^2\) è la somma dei quadrati dei valori di \(x\),
• \(\sum (x_i y_i)\) è la somma dei prodotti \(x_i y_i\). 

Poi calcolo dell'intercetta \( q \):

$$ q = \frac{\sum y_i - m \sum x_i}{n} $$

A questo punto, una volta determinati \( m \) e \( q \), posso scrivere l'equazione della retta di regressione.

$$ y = mx + q $$

Quest'ultima è la funzione lineare che approssima meglo i dati.

Nota. Il metodo dei minimi quadrati si può estendere anche a modelli polinomiali (curve anziché rette) o a modelli più complessi utilizzando una versione del metodo più avanzata detta dei minimi quadrati generalizzati.

Un esempio pratico

Ecco un esempio pratico di come funziona il metodo dei minimi quadrati per la regressione lineare.

Ho i seguenti dati sperimentali relativi a una variabile indipendente \(x\) e una variabile dipendente \(y\):

x	y
1	2
2	3
3	5
4	4
5	6

Questi $ n = 5 $ punti appaiono sparpagliati sul piano.

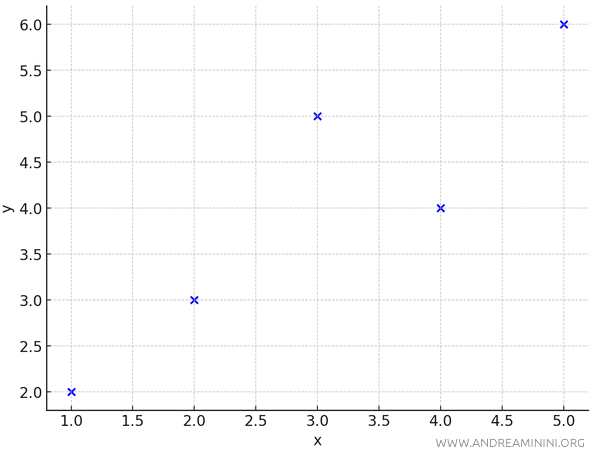
Voglio trovare la retta di regressione \(y = mx + b\) che meglio approssima questi punti.

Utilizzo la formula seguente per trovare il coefficiente angolare $ m $ della retta.

$$ m = \frac{n \sum (x_i y_i) - \sum x_i \sum y_i}{n \sum x_i^2 - (\sum x_i)^2} $$

Calcoliamo i valori necessari:

$$ \sum x_i = 1 + 2 + 3 + 4 + 5 = 15 $$

$$ \sum y_i = 2 + 3 + 5 + 4 + 6 = 20 $$

$$ \sum x_i^2 = 1^2 + 2^2 + 3^2 + 4^2 + 5^2 = 55 $$

$$ \sum (x_i y_i) = (1 \cdot 2) + (2 \cdot 3) + (3 \cdot 5) + (4 \cdot 4) + (5 \cdot 6) = 2 + 6 + 15 + 16 + 30 = 69 $$

Sapendo che $ n = 5 $, sostituisco questi valori nella formula del coefficiente angolare

$$ m = \frac{n \sum (x_i y_i) - \sum x_i \sum y_i}{n \sum x_i^2 - (\sum x_i)^2} $$

$$ m = \frac{5 \cdot 69 - 15 \cdot 20}{5 \cdot 55 - 15^2} $$

$$ m = \frac{345 - 300}{275 - 225} = \frac{45}{50} $$

$$ m = 0.9 $$

Il coefficiente angolare \(m = 0.9\) indica che per ogni aumento di 1 unità di \(x\), \(y\) aumenta di circa 0.9 unità.

A questo punto utilizzo la formula per calcolare l'intercetta $ q $

$$ q = \frac{\sum y_i - m \sum x_i}{n} $$

$$ q = \frac{20 - 0.9 \cdot 15}{5} $$

$$ q = \frac{20 - 13.5}{5} $$

$$ q = \frac{6.5}{5} $$

$$ q = 1.3 $$

L'intercetta \(q = 1.3\) è il valore di \(y\) quando \(x = 0\).

Ora che conosco sia il coefficiente angolare \(m = 0.9 \) che l'intercetta \( q=1.3 \), posso scrivere l'equazione della retta di regressione:

$$ y = mx + q $$

$$ y = 0.9x + 1.3 $$

La retta \(y = 0.9x + 1.3\) è la migliore approssimazione lineare dei dati secondo il metodo dei minimi quadrati.

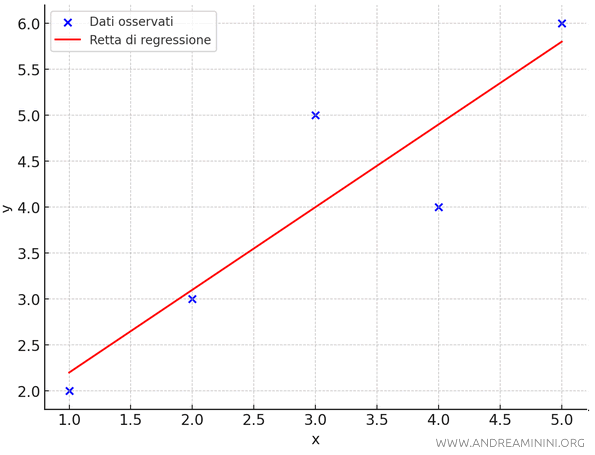
Questa retta riduce al minimo la somma dei quadrati degli errori tra i valori osservati \(y_i\) e i valori previsti \(y_{\text{previsti}}\).

x	y	yprevisto	e = y - yprevisto	e2
1	2	2.2	-0.2	0.04
2	3	3.1	-0.1	0.01
3	5	4.0	1.0	1.00
4	4	4.9	-0.9	0.81
5	6	5.8	0.2	0.04

In questo caso la somma dei quadrati degli errori parziali è

$$ S(m, b) = \sum_{i=1}^{n} \left( y_i - (mx_i + b) \right)^2 $$

$$ S(0.9, 1.3) = (2-2.2)^2 + (3-3.1)^2 + (5-4)^2 + (4-4.9)^2 + (6-5.8)^2 $$

$$ S(0.9, 1.3) = (-0.2)^2 + (-0.1)^2 + (1.0)^2 + (-0.9)^2 + (0.2)^2 $$

$$ S(0.9, 1.3) = 0.04 + 0.01 + 1.0 +0.81 + 0.04 $$

$$ S(0.9, 1.3) = 0.04 + 0.01 + 1.0 +0.81 + 0.04 $$

$$ S(0.9, 1.3) = 1.9 $$

In conclusione, non c'è un'altra retta in grado di ridurre ulteriormente la somma dei quadrati degli errori parziali. 

E così via.