La differenza tra interpolazione e regressione

L’interpolazione si concentra sull’approssimazione di valori mancanti all'interno dell’intervallo dei dati disponibili. La regressione è, invece, uno strumento per la previsione dei valori al di fuori dell'intervallo dei dati disponibili.

La differenza tra interpolazione statistica, matematica e regressione riguarda l'approccio e l'uso specifico di ciascuna tecnica per stimare o modellare i dati.

• Interpolazione matematica
  L'interpolazione matematica è una tecnica utilizzata per costruire una funzione continua \( f(x) \) che passa esattamente attraverso un insieme di punti noti \( (x_i, y_i) \). È usata quando conosco esattamente i valori in determinati punti e voglio stimare i valori intermedi. Le tecniche comuni includono l'interpolazione lineare tra due punti o polinomiale attraverso più punti.
  

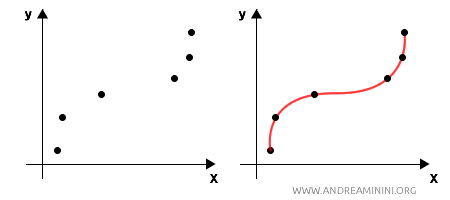
  Esempio: Se ho tre punti \((1, 2)\), \((2, 3)\), e \((3, 5)\), l'interpolazione polinomiale può costruire un polinomio di secondo grado che passa esattamente per questi tre punti.

• Interpolazione statistica
  L'interpolazione statistica è simile a quella matematica ma è applicata quando i dati sono osservazioni campionarie soggette a variabilità o rumore. Invece di passare esattamente per ogni punto, la funzione $ f(x) $ dell'interpolazione statistica non passa necessariamente per i punti osservati. In questo caso la retta o la curva continua passa vicino ai punti. È utile per creare una stima "smussata" dei valori intermedi all'interno dell'intervallo dei dati osservati.
  
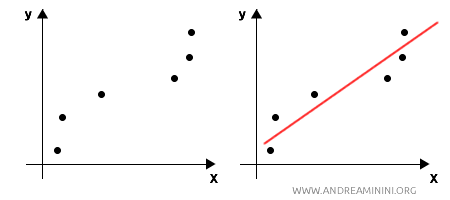
  È usata per stimare i valori intermedi tra punti noti, considerando l'incertezza o la variabilità dei dati, ma si limita generalmente all'intervallo dei dati osservati. Non è pensata per fare previsioni al di fuori dell'intervallo dei dati conosciuti (extrapolazione), perché non costruisce un modello che possa generalizzare su dati esterni al campione.

  Ad esempio, se conosco i dati della temperatura misurata a diverse ore del giorno, l'interpolazione statistica può stimare la temperatura tra due misurazioni, ma non è progettata per prevedere la temperatura in giorni futuri o fuori dall'intervallo delle misurazioni raccolte.

• Regressione
  La regressione è una tecnica statistica utilizzata per modellare la relazione tra una variabile dipendente (variabile di risposta) e una o più variabili indipendenti (predittori). A differenza dell'interpolazione matematica, la regressione non cerca di passare esattamente per tutti i punti, ma cerca invece di individuare la tendenza generale nei dati. L'obiettivo è trovare la funzione che meglio approssima i dati, anche al di fuori dell'intervallo dei punti osservati.
  
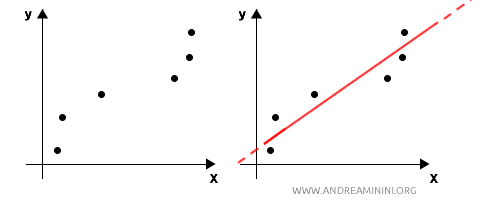
  Quindi, l'obiettivo della regressione è soprattutto predittivo, ossia prevedere l'andamento dei dati in futuro. Il modello di regressione non solo cerca di spiegare i dati osservati ma viene anche usato per predire il comportamento futuro o per stimare valori non osservati. In genere si cerca una funzione $ f(x) $ che minimizza la somma dei quadrati delle differenze tra i valori osservati e quelli stimati (metodo dei minimi quadrati). La funzione può essere lineare (regressione lineare), polinomiale (di grado superiore) o basata su modelli più complessi (es. regressione logistica, regressione non lineare, ecc.).

  Ad esempio, costruisco un modello di regressione lineare per predire i prezzi delle case in base a variabili come la superficie, il numero di stanze, e la posizione. Questo modello mi permette di predire il prezzo di una casa con caratteristiche simili ma che non è stata ancora osservata.

Riassumendo, l'interpolazione matematica e statistica sono usate quando si vuole stimare i valori intermedi dei dati, ma la prima assume che passi esattamente per i dati osservati, mentre la seconda tiene conto del rumore ed è più approssimativa.

La regressione, invece, cerca di individuare un modello che descriva la tendenza generale dei dati, senza necessariamente passare attraverso i singoli punti, anche al di fuori dell'intervallo dei dati osservati.

E così via.