Distribuzione campionaria

La distribuzione campionaria è la distribuzione di probabilità di una statistica, come la media o la varianza, ottenuta da più campioni casuali di uguale dimensione prelevati da una popolazione.

In altre parole, descrive come una certa statistica varia con il campionamento.

Per costruire una distribuzione campionaria seguo questi passaggi:

• Campionamento
  Estraggo un certo numero di campioni dalla popolazione (N). Ogni campione deve avere la stessa dimensione (n), ossia lo stesso numero di elementi. Per ogni campione calcolo una statistica come la media campionaria, la varianza, ecc. Ripeto più volte l'operazione.
• Distribuzione della statistica
  Le statistiche calcolate per ogni campione si distribuiscono su una gamma di valori. Questa è la distribuzione campionaria della statistica.

Un esempio comune è la distribuzione campionaria della media: se prendo tanti campioni di una certa dimensione da una popolazione e calcolo la media $ \bar{x} $ di ciascun campione, otterrò una distribuzione delle medie campionarie $ \bar{X} $ che solitamente si avvicina a una distribuzione normale o gaussiana.

• La media della distribuzione campionaria $ \mu_{ \bar{X} } $, ovvero la media aritmetica di tutte le medie, è una stima approssimativa della media $ \mu $ della popolazione.
• L'errore standard indica come variano i valori della distribuzione intorno al valore medio $ \mu_{ \bar{X} } $  $$ \sigma_{ \bar{X} } = \frac{\sigma}{\sqrt{n}}  $$ Dove \( \sigma \) è la deviazione standard della popolazione e \( n \) è la dimensione del campione.

La distribuzione campionaria è molto utile in statistica inferenziale, perché mi permette di stimare parametri della popolazione e calcolare intervalli di confidenza o test di ipotesi.

Nota. Secondo il teorema centrale del limite, se il campione è sufficientemente grande, la distribuzione campionaria della media campionaria tende ad avvicinarsi a una distribuzione normale, indipendentemente dalla distribuzione della popolazione di partenza.

Un esempio pratico

Devo studiare l'altezza media di tutti gli studenti di una scuola, ma non ho accesso ai dati di tutti gli studenti.

Quindi, decido di prelevare dei campioni casuali di studenti e calcolare l'altezza media per ciascun campione.

Supponiamo che la scuola abbia 1.000 studenti e che l'altezza media dell'intera popolazione sia di 170 cm, con una deviazione standard di 10 cm.

Estaggo casualmente dei campioni di 30 studenti (di dimensione \(n = 30\)) e per ogni campione calcolo l'altezza media.

Ogni volta che prelevo un campione diverso, ottengo una media campionaria diversa. Per esempio:

• Primo campione: media campionaria = 168 cm
• Secondo campione: media campionaria = 172 cm
• Terzo campione: media campionaria = 169 cm
• E via dicendo...

Dopo aver prelevato molti campioni, costruisco una serie con tutte le medie campionarie ottenute.

Queste medie campionarie formano una nuova distribuzione, chiamata distribuzione campionaria della media.

Questo è il grafico della distribuzione campionaria della media.

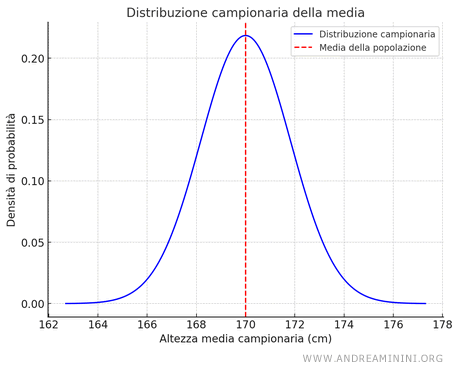
Nota. La curva della distribuzione campionaria è vicina a una distribuzione normale (gaussiana), dove la linea tratteggiata rappresenta la media della popolazione (170 cm). L'asse verticale misura la frequenza con cui si verifica un determinato valore della media campionaria.

La distribuzione campionaria delle medie ha le seguenti caratteristiche:

• La media della distribuzione campionaria è vicina alla media della popolazione, cioè 170 cm.
• La varianza della distribuzione campionaria della media è più piccola rispetto alla varianza della popolazione. La deviazione standard della distribuzione campionaria, chiamata errore standard, è: $$ \sigma_{ \bar{X} } = \frac{\sigma}{ \sqrt{n}} $$ Ad esempio, se \( \sigma=10 \ cm \) e \( n=30 \)  l'errore standard è: $$ \sigma_{ \bar{X} } = \frac{10}{\sqrt{30}} \approx 1.83 \  cm $$ 

Quindi, anche se la distribuzione delle altezze nella popolazione non è normale, grazie al teorema centrale del limite la distribuzione delle medie campionarie segue approssimativamente una distribuzione normale.

La proprietà di non distorsione della media campionaria

Se prendo tutti i possibili campioni di una data dimensione \(n\) dalla popolazione (o un numero molto grande di campioni casuali) e calcolo la media per ogni campione, la media di tutte le medie campionarie è uguale alla media vera della popolazione.

In altre parole, la media di tutte le medie campionarie coincide con la media della popolazione

Questo è uno dei risultati fondamentali della statistica e si basa sulla proprietà di non distorsione (unbiasedness) della media campionaria.

Matematicamente, se \( \mu \) è la media della popolazione e \( \bar{x}_i \) è la media del campione \(i\), allora:

$$ \mathbb{E}(\bar{X}) = \mu $$

Dove \( \mathbb{E}(\bar{X}) \) è il valore atteso della media campionaria, che coincide con la media della popolazione \( \mu \).

Questo è vero per qualsiasi dimensione del campione \(n\), e non dipende dalla distribuzione della popolazione, purché i campioni siano indipendenti e casuali.

Il risultato dimostra che la distribuzione campionaria è uno stimatore corretto della media della popolazione.

Cos'è uno stimatore corretto? Uno stimatore corretto è uno strumento che, in media, mi fornisce il valore vero del parametro che voglio stimare. Ciò significa che non introduce errori sistematici e, con l'aumentare delle osservazioni campionarie, i suoi risultati si avvicinano sempre di più al valore reale.

Nella pratica, non è necessario estrarre tutte le possibili combinazioni di campioni di una certa dimensione; è sufficiente prelevarne un gran numero.

La legge dei grandi numeri garantisce che, anche con una parte dei campioni, la media delle medie campionarie sarà molto vicina alla media della popolazione.

Esempio. Se i campioni hanno dimensione \(n = 30\) e la popolazione è composta da \(N = 1000\) elementi, lo spazio campionario, nel caso di campionamento con ripetizione e con elementi ordinati, è composto da \(1000^{30}\) combinazioni. Tuttavia, non è necessario considerare tutte le possibili combinazioni. Anche con un numero sufficientemente grande di campioni casuali, posso ottenere lo stesso risultato, poiché la media campionaria è uno stimatore non distorto della media della popolazione.

Il teorema centrale del limite

Per campioni casuali di dimensione \(n\) sufficientemente grande, la distribuzione della somma o della media campionaria \( \bar{X} \) delle osservazioni tende a una distribuzione normale, indipendentemente dalla distribuzione della popolazione di partenza, a patto che la varianza \( \sigma^2 \) della popolazione sia finita.

In altre parole, man mano che la dimensione del campione \(n\) aumenta, la distribuzione della media campionaria tende a una distribuzione normale, indipendentemente dalla forma della distribuzione della popolazione da cui sto campionando.

Questo fenomeno accade perché, quando il numero di osservazioni \( n \) nel campione aumenta, le variazioni casuali tendono a "compensarsi" e la distribuzione della media campionaria diventa più simmetrica e a forma di campana (normale).

Quindi, anche se la popolazione di partenza non segue una distribuzione normale, la media dei campioni casuali tende a farlo.

Nota. Questa proprietà è estremamente utile in statistica, poiché mi permette di usare la distribuzione normale per fare inferenza (come calcolare intervalli di confidenza e test di ipotesi) anche quando non conosco la distribuzione della popolazione originale.

E così via.