Intervallo di confidenza
Un intervallo di confidenza è un range di valori utilizzato in statistica per stimare un parametro della popolazione (ad esempio, la media \( \mu \)) con un certo livello di certezza.
In altre parole, un intervallo di confidenza è un intervallo di valori che probabilmente contiene il vero valore di un parametro della popolazione, come la media μ, con un certo grado di certezza statistica.
È utile perché mi fornisce una misura dell'incertezza legata a una statistica campionaria, come la media \( \bar{x} \), che serve a stimare la vera media della popolazione \( \mu \).
La formula dell'intervallo di confidenza
La formula generale per un intervallo di confidenza per la media \( \mu \), nel caso di una distribuzione normale e con varianza nota, è data da:
$$ \bar{x} \pm z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} $$
Dove:
- \( \bar{x} \) è la media campionaria,
- \( z_{\alpha/2} \) è il valore critico corrispondente al livello di confidenza desiderato (ad esempio, 1.96 per il 95%),
- \( \sigma \) è lo scarto quadratico medio della popolazione (o la sua stima),
- \( n \) è la dimensione del campione.
Nota. Se la varianza della popolazione non è nota, per calcolare l'intervallo di confidenza è preferibile utilizzare la distribuzione \( t \) di Student al posto della distribuzione normale.
Per costruire un intervallo di confidenza, devo prima scegliere un livello di confidenza \( 1 - \alpha \).etro.
Il livello di confidenza indica la probabilità che l'intervallo calcolato contenga il vero valore del parametro della popolazione.
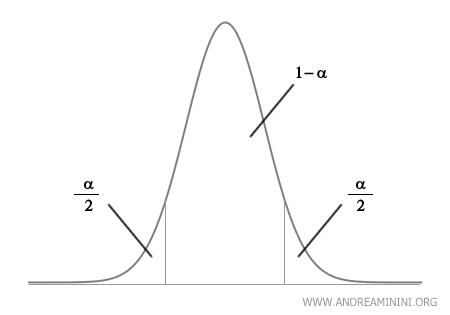
Il parametro \( \alpha \) è, invece, detto livello di significatività (o complemento del livello di confidenza) ed è la probabilità che l'intervallo non includa il vero valore del parametro
Ad esempio, un intervallo di confidenza con livello di confidenza \( 1 - \alpha = 95% \) è costruito in modo tale che, se ripetessi l'esperimento molte volte, il 95% degli intervalli calcolati includerebbe la vera media μ della popolazione. In questo caso il livello di significatività è\( 1 - 0.95 = 0.05 \), ossia il 5%. Questo significa che c'è una probabilità del 5% che l'intervallo calcolato non contenga il vero valore del parametro.
Pertanto, il livello di confidenza esprime il grado di fiducia che ho nella stima.
Un esempio pratico
Supponiamo di dover stimare la media \( \mu \) del peso degli studenti in una scuola con migliaia di iscritti.
Prendo un campione di 100 studenti, la cui media campionaria \( \bar{x} \) è di 70 kg e la deviazione standard della popolazione \( \sigma \) è nota ed è pari a 10 kg.
Scelgo di calcolare un intervallo di confidenza al 95% per la media del peso degli studenti.
La formula per l'intervallo di confidenza è:
$$ \bar{x} \pm z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} $$
Sapendo che la media campionaria è \( \bar{x} = 70 \), la deviazione standard della popolazione è \( \sigma = 10 \) e la numerosità del campione è \( n = 100 \)
$$ 70 \pm z_{\alpha/2} \cdot \frac{10}{\sqrt{100}} $$
Per un livello di confidenza del 95%, il valore critico \( z_{\alpha/2} \) in una distribuzione normale è 1.96.
$$ 70 \pm 1.96 \cdot \frac{10}{\sqrt{100}} $$
$$ 70 \pm 1.96 \cdot 1 $$
$$ 70 \pm 1.96 $$
Quindi, l'intervallo di confidenza è:
$$ [70 - 1.96, 70 + 1.96] = [68.04, 71.96] $$
Questo significa che, con un livello di confidenza del 95%, posso affermare che la media del peso degli studenti si trova tra 68.04 kg e 71.96 kg.
E così via.
